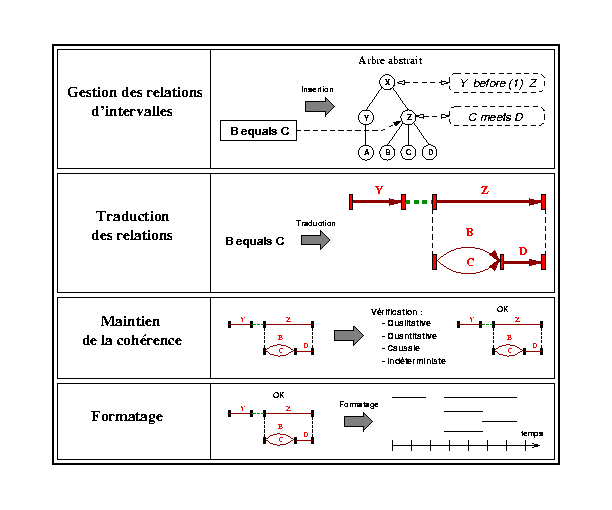
Le travail présenté ici se veut avant tout une contribution aux systèmes d'édition de documents multimédia. Nous avons souhaité exposer d'abord dans le Chapitre III le raisonnement temporel dans le cadre plus général des systèmes de contraintes. En ce qui concerne l'application Madeus, nous avons accordé une attention particulière à deux aspects, l'incrémentalité et une certaine approche du temps. Comme on se place dans un environnement d'édition interactif, les différents traitements des contraintes temporelles doivent être faits par une manipulation incrémentale. D'autre part, il est nécessaire de prendre en compte l'aspect causal et indéterministe du temps inhérents à une présentation multimédia. Les propositions faites dans ce chapitre constituent une première solution dont le but est de permettre la construction d'une application d'édition et de présentation opérationnelle, Madeus. Elles ne prétendent pas résoudre toutes les difficultés théoriques posées, qui dépassent largement le cadre de cette thèse.
Dans la première section, nous présentons une vue d'ensemble du module de gestion de contraintes temporelles, appelé gestionnaire temporel. La section 2 est consacrée à la description des éléments de base, des relations temporelles supportées et à leur représentation interne sous forme d'un graphe d'instants qui constitue aussi notre réseau de contraintes, nous parlerons de graphe de contraintes. Dans la dernière section, les algorithmes de gestion des relations sont développés. Ces algorithmes forment le coeur de la phase d'édition de Madeus. Leur rôle est de produire une forme exécutable du document. À partir de cette forme, le module de présentation peut alors ordonnancer la présentation. Ceci fait l'objet du chapitre VI.
Au delà de la difficulté théorique inhérente aux problèmes de synchronisation temporelle, une mise en oeuvre efficace d'une application d'édition multimédia doit offrir une réponse adaptée aux problèmes qui viennent du processus d'édition/présentation :
Avant d'aborder en détail les traitements réalisés
par le gestionnaire temporel, nous présentons dans cette section
une vue d'ensemble de son architecture logicielle.

Le gestionnaire temporel de Madeus est organisé sous forme de quatre modules dont chacun assure une fonction particulière du système d'édition et de présentation :
Chaque intervalle est décrit par une borne inférieure l (lower bound) et une borne supérieure u (upper bound) et est noté [l, u] (où l < u, l et u sont des valeurs positives et u pouvant valoir l'infini).
Les intervalles considérés dans Madeus peuvent être
de deux types contrôlables ou incontrôlables
:
Définition 1 : Un intervalle contrôlable
est un intervalle ayant une contrainte numérique sur la durée
delta = [l,u]c , et cette contrainte peut être
réduite librement par le système d'édition entre l
et u.
Ce type d'intervalle permet de modéliser le comportement des
éléments de type continu et discret dont la durée
de présentation peut être choisie dans un certain intervalle.
Cette durée est bornée pour les éléments continus
par des limites liées à l'intelligibilité de leur
contenu, mais pour les éléments discrets comme le texte et
les graphiques, elle peut être infinie. Ce type d'intervalle présente
un comportement temporel élastique.
Définition 2 : Un intervalle incontrôlable
est un intervalle ayant une contrainte numérique sur la durée
omega = [l,u]i , et cette contrainte n'est connue qu'à
l'exécution.
Ce type d'intervalle permet de modéliser le comportement indéterministe de certains éléments multimédia dont la durée de présentation ne peut être connue pendant la phase d'édition. Par exemple, pour les boutons d'interaction , la durée qui leur est associé correspondant à la période de temps ou ils sont activables, mais la valeur effective de ces durées ne dépend que de l'instant même de leur activation.
D'après ces deux types d'intervalles, nous pouvons distinguer deux propriétés qui caractérisent le scénario temporel d'un document multimédia : la flexibilité et la contrôlabilité.
La flexibilité mesure l'aptitude d'un scénario temporel à pouvoir être adapté aux contraintes numériques induites par les spécifications de l'auteur tout en garantissant sa cohérence globale. La flexibilité d'un scénario dépend de l'élasticité des éléments multimédia (définie par la différence u-l des intervalles contrôlables) présents dans le document ainsi que de leur emplacement dans le graphe de contraintes.
Cette flexibilité du document peut être mise à profit pour compenser le comportement indéterministe qu'il contient (cf. 3.2.4). Cela introduit la notion de contrôlabilité qui mesure l'aptitude d'un scénario à pouvoir être adapté dynamiquement, à l'exécution, au comportement indéterministe des éléments multimédia qu'il contient. Il s'agit donc d'une généralisation de la notion de cohérence pour les scénarios indéterministes [VID 97].
Dans Madeus, l'arbre abstrait est défini par un ensemble d'éléments multimédia de base ou composés où :
rn (e1,.. ,en) ==> forall i (1 <= i < n) ei r ei+1
Graphe de contraintes
À partir de l'arbre abstrait (voir exemple dans la Fig 1 ) et les relations à base d'intervalles, nous définissons, pour chaque élément composé d'un document, un graphe de contraintes G = (I, A, E) à base d'instants, de la façon suivante :
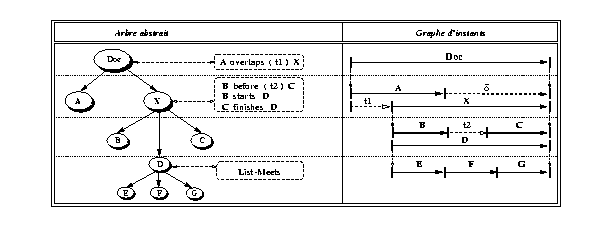
Deux instants abstraits de début et de fin sont attachés aux éléments composés du document, afin de délimiter leur contenu dans le temps. Ceci permet de définir pour chaque élément composé c un sous-graphe de contraintes Gc = (Ic, Ac, Ec) qui est construit de la même façon que celui du document lui-même. Ainsi, nous pouvons ramener le traitement temporel pour tout un document à celui d'un seul niveau de la hiérarchie logique. Le graphe obtenu est orienté (voir Fig 1 ) et acyclique (Directed Acyclic Graph : DAG) (voir la condition de cohérence qualitative présentée dans la section 3.2.1). À chaque niveau de la hiérarchie logique, le graphe de contraintes correspondant possède un seul sommet source (l'instant début de l'élément englobant) et un seul sommet puit (l'instant de fin de l'élément englobant).
Chaînes temporelles
Le graphe G étant à base d'instants, il nous permet d'en avoir une vue supplémentaire sous forme d'un ensemble de chaînes temporelles. Ces chaînes sont définies de la façon suivante :
Définition : Une chaîne temporelle Ch={a1,.. , an} est une séquence d'arcs contigus du graphe G tels que chaque arc aj, 2 < j < n-1, n'est relié qu'à un seul arc prédécesseur et à un seul arc successeur. De plus, le sommet a+j-1 est confondu avec le sommet a-j, chaque arc étant étiqueté par un intervalle contrôlable ou incontrôlable.
À toute chaîne Ch = {a1,.. , an} , telle que aj est étiqueté par [lj, uj] dans le graphe, nous pouvons associer comme étiquette l'intervalle suivant :
[ [Here is a formula]j , [Here is a formula]j ]
On peut ainsi définir un graphe de chaînes noté
GCh, obtenu à partir du graphe G en remplaçant
la suite des arcs composant une chaîne Ch par l'arc Ch dans GCh
(Fig 2 ).
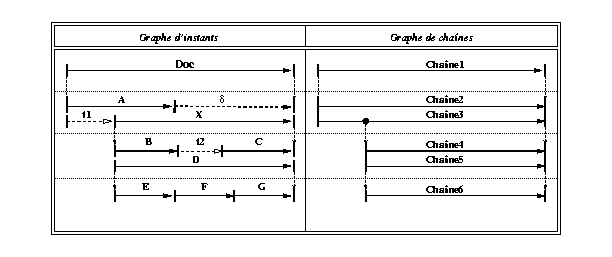
L'intérêt de cette structuration en chaînes dans Madeus est principalement lié à deux considérations. Elle permet d'améliorer les performances des opérations de mise à jour du document, car la plupart des traitements portent sur des chaînes et non pas directement sur des intervalles, en particulier, en ce qui concerne la vérification de la cohérence. Par ailleurs, les chaînes peuvent être mises à profit pour gérer l'indéterminisme pendant l'édition et pendant la présentation puisqu'elles constituent les branches parallèles du scénario.
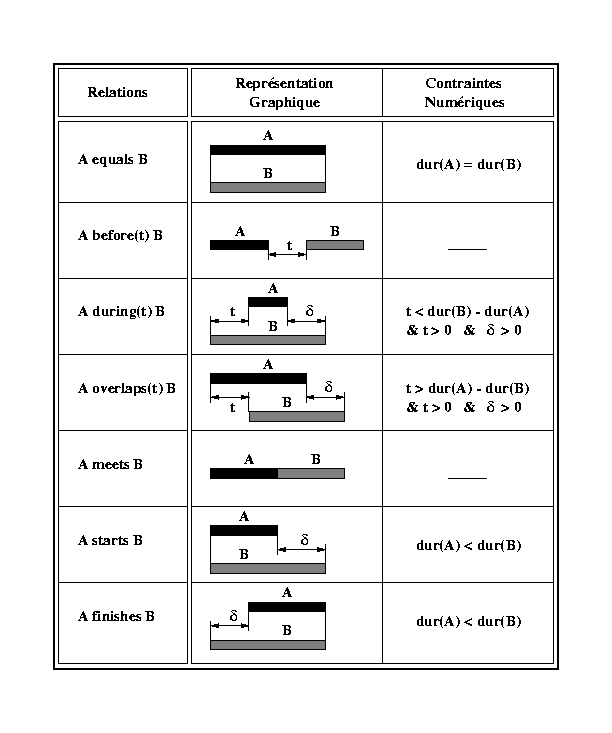
La sémantique de ces relations est définie par un ensemble de contraintes entre les instants de début et de fin des intervalles. Ces contraintes font intervenir la durée et le type (contrôlable ou non) des intervalles associés aux éléments multimédia du document. La Fig 3 illustre la correspondance entre les relations d'intervalles d'Allen, dotée éventuellement d'un paramètre quantitatif de durée, et leur représentation sous forme d'un graphe à base d'instants, avec les contraintes associées. Les lignes verticales de la Fig 3 représentent des contraintes de simultanéité entres les différents instants qui interviennent dans les relations.
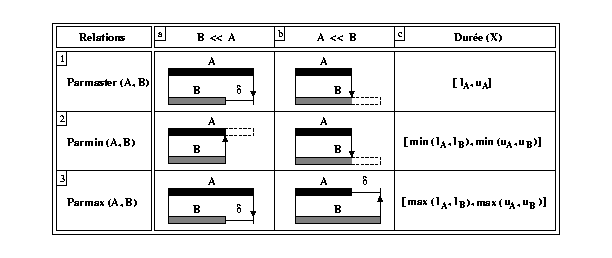
Les relations causales dans Madeus ont la sémantique suivante :
Pour A = [lA, uA], B = [lB, uB], ( lA, uA, lB, uB > 0 ), A << B ==> uA < lB
Cet ordre nous permet de déterminer laquelle des deux situations se présente. En particulier, lors de la transformation des relations Parmaster et Parmax en relations d'instants, nous pouvons savoir s'il faut ou non insérer un délai et à quel endroit du graphe. Dans le cas où l'ordre << ne peut être établi, le problème peut être contourné en encapsulant dans un élément composé X les deux intervalles A et B ainsi que la relation correspondante. Ensuite, le traitement avec le reste du document est réalisé à partir de cette nouvelle entité. Dans ce cas, l'intervalle associé à l'élément composé X, qu'il soit contrôlable où incontrôlable, possède des bornes de durées bien définies (voir la colonne c de la Fig 4 ). Dans la section 3.2.2, nous montrons comment le type (contrôlable ou incontrôlable) de l'intervalle X est déterminé. Cette information intervient dans la méthode de vérification de la cohérence causale proposée.
Fonctions d'insertion et de suppression de relations
RelationId <== Crée_Relation (Parent, Intervalle1, TypeRelation, Paramètre_Temporel, Intervalle2).
Supprime_Relation (Parent, RelationId).
Ces deux fonctions permettent la création et la suppression d'une relation dans le document. L'opération d'insertion retourne l'identifiant interne d'une structure RelationId qui représente la relation et sa traduction sous forme de relations d'instants (voir la section 2.4).
Parent : désigne l'élément composé de la structure logique sur lequel on veut insérer la relation.
Intervalle1, Intervalle2 : sont les identifiants symboliques des intervalles liés par cette nouvelle relation.
TypeRelation : indique quel est le type de relation temporelle liant les deux intervalles (représentation interne des relations).
Paramètre_Temporel : indique la valeur du délai lié dans la relation temporelle en question (ce délai est null si la relation ne fait pas intervenir de délai).
L'intérêt de garder en mémoire la structure RelationId est double : d'une part, dans le cas d'incohérence, cette structure permet de retrouver la relation d'intervalle incriminée et permet donc de retourner le bon message d'erreur à l'utilisateur. D'autre part, étant donné que le format de stockage des documents est basé sur les intervalles, cette structure permet de retrouver aisément la forme finale du document à partie de l'arbre abstrait.
Dans la suite de cette section, nous présentons le traitement qui est effectué lors de l'appel des fonctions présentées. Comme les relations n-aires n'interviennent qu'au niveau du format du document, et que leur traitement se ramène à des relations binaires, nous nous limiterons à exposer ce dernier cas de figure.
Les relations d'instants données dans le tableau sont organisées selon une suite de relations i1 r1 i2 r2 i3 r3 i4. Chaque suite correspond à une entrée du tableau et représente la conjonction de relations d'instants : (i1 r1 i2), (i2 r2 i3) et (i3 r3 i4) où chaque instant i correspond à un sommet existant ou à créer dans le graphe de contraintes, c'est à dire (a-, a+, b-, ou b+).
Les entrées du tableau qui représentent les instants et les relations d'instants ont été disposées conformément à leur ordre d'apparition temporel dans la relation d'intervalle (ordre de précédence a- < a+ et b- < b+).
Les relations d'instants (i1 r i2) que nous utilisons sont les suivantes :
| Relation | i1 | r1 | i2 | r2 | i3 | r3 | i4 |
|---|---|---|---|---|---|---|---|
| a finishes b | b- | < | a- | < | a+ | = | b+ |
| a starts b | a- | = | b- | < | a+ | < | b+ |
| a overlaps b | a- | < | b- | < | a+ | < | b+ |
| a during b | b- | < | a- | < | a+ | < | b+ |
| a meets b | a- | < | a+ | = | b- | < | b+ |
| a before b | a- | < | a+ | < | b- | < | b+ |
| a equals b | a- | = | b- | < | a+ | = | b+ |
| parmax(a, b) | a- | = | b- | < | a+ | hookleftarrow | b+ |
| parmaster(am, b) | am- | = | b- | < | am+ | ==> | b+ |
| parmin(a, b) | a- | = | b- | < | a+ | leftrightarrow | b+ |
Les relations '=', '==>', 'leftrightarrow' et 'hookleftarrow' entre deux instants i1 et i2 entraînent leur fusion sur un même sommet du graphe G. La relation '<' entraîne la création d'un arc entre les sommets i et j. Dans la suite de ce chapitre, on désignera un sommet par i ou j et on désignera l'arc reliant i à j par (i, j).
Dans l'application Madeus, la redéfinition ou l'ajout de nouvelles définitions de relations temporelles se limite à la simple mise à jour de cette table. Cela permet, à tout moment, de modifier les relations temporelles supportées et l'interface graphique d'édition (palette de relations) sans avoir à apporter de grands changements aux traitements effectués par l'application.
Les mises à jour du document ont généralement une portée locale. Cette portée est délimitée par les instants de début et de fin associés aux éléments. Les modifications introduites dans la structure temporelle susceptibles d'avoir lieu après chaque type d'opération d'édition sont détaillées dans la section 3.1. Ce sont ces opérations qui permettent la construction incrémentale du graphe par des mises à jour locales, et c'est à partir de ces mises à jour qu'on peut déterminer la portion du graphe qui doit être vérifiée.
Vérifier_et_ajouter_relation (RelationId)
{
1. Si (Relation_cohérente_a_priori (Relation_Id))
2. Alors Créer_sommets(RelationId);
3. Relier_sommets_au_graph(RelationId);
4. Propager_contraintes();
5 Sinon /* incohérence détectée */
6. Retourner_erreur(RelationId);
}
La fonction Créer_sommets() effectue la création de nouveaux sommets pour les intervalles A et B de la relation, s'ils ne sont pas déjà créés. Ces sommets sont les représentants de l'élément A et B dans le graphe de contraintes. Comme ce graphe est structuré en chaînes, les sommets des intervalles A et B sont d'abord regroupés dans des chaînes (une pour chaque intervalle Fig 7 ) avant d'être insérés dans le graphe par la fonction Relier_sommets_au_graphe().
La fonction Relier_sommets_au_graphe() modifie la structure de graphe en y apportant les trois types de mise à jour cités auparavant : la création de sommets, l'insertion d'arcs ou la fusion de sommets existants du graphe. Ces opérations affectent la configuration des chaînes existantes et/ou en créent de nouvelles. Les algorithmes de vérification s'appuient sur ces chaînes pour déterminer la cohérence de la relation insérée. Pour cette raison, les procédures mettant en oeuvre ces trois opérations retournent la liste des chaînes modifiées.
Fusion de sommets
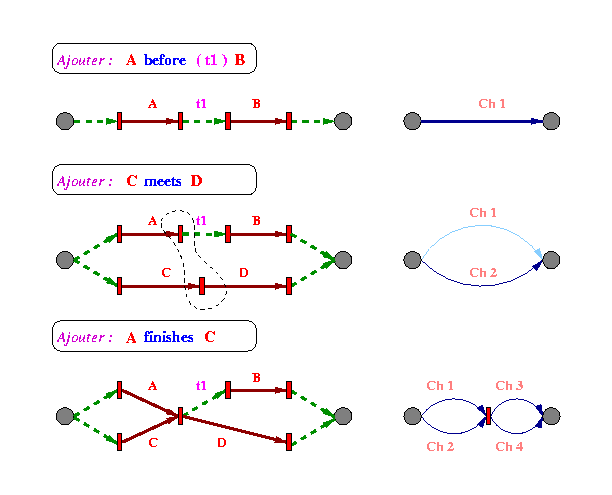
Dans ce qui suit, nous détaillons l'opération de fusion de sommets qui présente la plus grande complexité. Pour comprendre cet algorithme, nous allons dérouler pas à pas un exemple d'enchaînements d'insertion de relations.
L'exemple de la Fig 7 , donne une illustration
graphique du fonctionnement de l'algorithme d'insertion de relations pendant
une session d'édition. Au début le document est vide et l'auteur
insère une relation A before (t1) B. Cette opération a pour
effet l'apparition dans le graphe des arcs représentant A et B ainsi
que le délai t1, sous forme d'une chaîne Ch1. Ensuite, l'insertion
de la relation C meets D a pour conséquence l'apparition d'une chaîne
parallèle Ch2, et ainsi de suite. L'insertion de la relation A finishes
C dans notre exemple a engendré la fusion de deux sommets, produisant
ainsi les quatre chaînes (Ch1, .., Ch4).
L'opération de fusion de deux sommets, qui intervient lorsqu'il
y a une relation d'instant de type '=', 'leftrightarrow', '==>' ou 'hookleftarrow'
entre eux, est gérée par l'algorithme présenté
dans la Fig 8 . Cet algorithme prend en entrée
deux sommets s1 et s2 à fusionner. Il commence d'abord par éliminer
les délais temporels qui peuvent éventuellement relier chacun
de ces sommets au début ou à la fin de l'élément
englobant (lignes 3-6 de l'algorithme). Ensuite, une phase supplémentaire
permet de diviser les chaînes correspondant aux sommets s1 et s2
en deux chaînes chacune (lignes 8-11). Celles-ci sont ensuite fusionnées
sur un seul sommet s qui regroupe toutes les chaînes entrantes et
sortantes de s1 et s2 (ligne 12). L'algorithme enregistre sur le sommet
s la relation d'instant qui fait intervenir les extrémités
des chaînes des sommets s1 et s2 (lignes 13-22) : la raison de la
fusion. Enfin, si le résultat des modifications entraîne la
création de deux chaînes, il les concatène pour en
produire une seule (lignes 23-27).
Chaînes <== Fusionner_sommets ( s1, s2, Relation_instant )
{
1. /* Enlever les intervalles de délai reliant les sommets */
2. /* s1 et s2 aux instants source et puit de l'englobant */
3. Enlever_arc_depuis_début(s1);
4. Enlever_arc_depuis_début(s2);
5. Enlever_arc_depuis_fin(s1);
6. Enlever_arc_depuis_fin(s2);
7. /* Phase initiale de la fusion de deux sommets */
8. si (Degré_entrant(s1) = Degré_sortant(s1) = 1)
9. Diviser_chaîne_en_deux(s1);
10. si (Degré_entrant(s2) = Degré_sortant(s2) = 1)
11. Diviser_chaîne_en_deux(s2);
12. s <== Fusionner_sommets(s1, s2);
13. pour (Relation_instant) {
14. '=':
15. Ajouter_relation_au_sommet(s,(=,Chaîne(s1),Chaîne(s2)))
16. '==>':
17. Ajouter_relation_au_sommet(s,(==>,Chaîne(s1),Chaîne(s2)))
18. 'leftrightarrow':
19. Ajouter_relation_au_sommet(s,(leftrightarrow,Chaîne(s1),Chaîne(s2)))
20. 'hookleftarrow':
21. Ajouter_relation_au_sommet(s,(hookleftarrow,Chaîne(s1),Chaîne(s2)))
22. }
23. si (Degré_entrant(s) = Degré_sortant(s) = 1) {
24. Chaîne1 = Chaîne_de_sommet_de_fin(s);
25. Chaîne2 = Chaîne_de_sommet_de_début(s);
26. Concaténer_chaînes(Chaîne1, Chaîne2);
27. }
28. Retourner (Toutes_les_chaînes_modifiées)
}
En plus de sa fonction de construction du graphe, cet algorithme permet d'identifier les contraintes numériques à vérifier. Il s'agit des contraintes liées aux intervalles des nouvelles chaînes créées et/ou modifiées du graphe. Nous pouvons ainsi limiter le traitement de la cohérence aux seules chaînes en question. Dans l'exemple de la Fig 7 , cela revient à s'assurer que les contraintes Ch1 = Ch2 et Ch3 = Ch4 peuvent être vérifiées. Pour cette raison, l'algorithme retourne la liste des chaînes créées ou modifiées afin de les passer aux algorithmes de vérification détaillés dans la section 3.2.
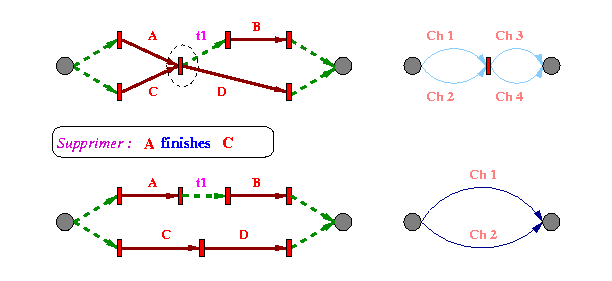
Les deux premières opérations consistent à effectuer le traitement inverse de celui réalisé par l'algorithme de la Fig 8 . Signalons que les intervalles qui interviennent dans chaque relation supprimée ne disparaissent effectivement du graphe que s'ils ne figurent dans aucune autre relation du document (c'est le cas par exemple de l'intervalle A dans Fig 9 ). Pour obtenir cette information, un compteur de références est utilisé, qui indique le nombre de fois qu'un intervalle figure dans une relation. Ce compteur est incrémenté/décrémenté à chaque insertion/suppression de relation qui met en jeu l'intervalle. Dès que ce compteur atteint la valeur nulle, l'intervalle en question et éventuellement les sommets du graphe correspondants sont supprimés.
La suppression d'un élément du document revient aussi à la suppression de relations du document. En effet, cette suppression entraîne celles de toutes les relations dans lesquelles figure l'intervalle correspondant. Ce qui, comme nous venons de le montrer, a aussi pour effet de supprimer du graphe l'intervalle correspondant ainsi que de relâcher les contraintes numériques qu'il a pu apporter.
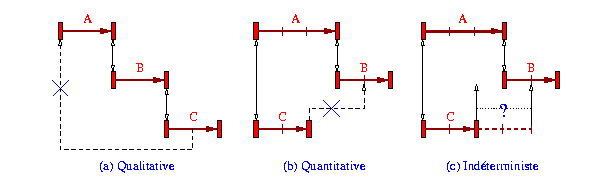
Supposons qu'une partie d'un document soit composée de trois
éléments A, B et C (voir. Fig 10 -a),
et que ces éléments soient liés par les relations
(A meets B) et (B meets C). L'adjonction d'une nouvelle spécification
C overlaps A rend le scénario incohérent. Ce cas correspond
à une incohérence de type qualitatif car elle ne dépend
pas des durées des éléments mais de la sémantique
même des relations mises en jeu. En revanche, un scénario
qui peut être cohérent du point de vue qualitatif peut être
quantitativement incohérent. Par exemple (voir Fig
10 -b), si l'auteur spécifie que (A meets B) et (A starts
C), l'adjonction de la relation (C overlaps B) rend le scénario
incohérent pour des durées de A, B et C valant respectivement
30, 20 et 20 secondes. Finalement, dans l'exemple de la Fig
10 -c, on reprend le scénario précédent, mais
avec un élément C dont l'intervalle de durée est de
type incontrôlable de valeur [20, 40]. Ce cas correspond à
une incohérence si, à l'exécution, la durée
de l'élément C prend une valeur dans l'intervalle [20,30],
par contre, le même scénario sera cohérent si la valeur
de cette durée est dans l'intervalle [30,40]. Ce cas est considéré
comme une incohérence car cette contrainte ne peut pas être
garantie dans tous les cas (cf. 3.2.4).
Dans des scénarios plus complexes, les incohérences sont moins faciles à détecter que pour les trois exemples précédents, à cause des effets indirects des contraintes. Dans l'approche structurée des documents multimédia, la structure logique arborescente du document réduit considérablement la portée de ces contraintes, et par là même celle de la vérification. En effet, les éléments de base se trouvant au niveau des feuilles de l'arbre, une gestion ascendante de la cohérence par propagation des contraintes fournit un mécanisme efficace adapté au processus incrémental de l'édition.
Dans la suite de cette section, nous présentons les solutions mises en oeuvre dans Madeus pour la vérification des quatre types de cohérence suivants :

Pour chaque relation d'intervalle introduite dans le document, la vérification de la cohérence qualitative consiste donc à vérifier que l'insertion de délais ainsi que la fusion des sommets qu'elle entraîne sur le graphe, n'introduisent pas de cycles. L'algorithme qui réalise cette fonction est décrit dans la Fig 12 . Notons qu'il n'est pas nécessaire de modifier le graphe pour réaliser cette opération (vérification a priori).
Dans cet algorithme, les instants i et j considérés sont
ceux qui interviennent dans la relation RelationId, c'est-à-dire,
si RelationId = (A R B), i, j in { A-, A+,B-,
B+}. Intervalle(i) est une fonction qui rend l'intervalle
auquel appartient l'instant i : Intervalle(i) = A / i = A+
ou i = A-. Sommet_du_graphe(i) est une fonction qui
retourne le sommet correspondant à i dans le graphe d'instants.
Boolean <== Cohérence_Qualitative (RelationId)
{
1. Pour chaque relation d'instants (i r j) in RelationId
2. si (Intervalle(i) =/= Intervalle(j)) et (r =/= ?)
3. alors s1 = Sommet_du_graphe(i)
4. s2 = Sommet_du_graphe(j)
5. si (Chemin_existe(s1, s2))
6. alors retourne (Faux) /*Cycle détecté*/
7. sinon retourne (Vrai)
}
Dans le cas de l'exemple précédent (Fig 11 ), la relation (C overlaps A) induit les relations d'instants : C- < A- < C+ < A+. Pour la relation i r j = C- < A-, s1 et s2 correspondent aux sommets du graphe représentant les instants i et j (fonction Sommet_du_graphe()), on a avec A- < C-, un cycle sur la même chaîne.
Pour empêcher la création de cycles, on vérifie s'il n'existe pas déjà un chemin dans le graphe entre les sommets que l'on doit relier lors de l'adjonction de la nouvelle relation (fonction Chemin_existe appelée dans Fig 12 ). Cet algorithme est basé sur deux aspects du graphe qui permettent d'accélérer la détection de chemin :
Booléen <== Chemin_existe (s1, s2)
{
1. /* les deux sommets sont sur la même chaîne temporelle */
2. si (Chaîne(s1) = Chaîne(s2))
3. retourne Vrai;
4. /* s'ils ne sont pas sur la même chaîne temporelle */
5. si rang(s1) < rang(s2)
6. sA = s1; sB = s2;
7. sinon sA = s2; sB = s1;
8. si (Degré_entrant(s1) = Degré_sortant(s1) = 1)
9. ch1 = Chaîne_du_sommet(s1)
10. sA = Sommet_de_fin_de_la_chaîne(ch1)
11. si (Degré_entrant(s2) = Degré_sortant(s2) = 1)
12. ch2 = Chaîne_de_sommet(s2)
13. sB = Sommet_de_début_de_la_chaîne(ch2)
14. si (sA = sB)
15 retourne Vrai /* cycle trouvé */
16.
sinon si rang(sA) >= rang(sB)
17. retourne Faux /* pas de cycles */
18. sinon
19. retourne Recherche_Chemin(sA, sB);
}
L'algorithme vérifie d'abord si les deux sommets se trouvent sur la même chaîne (2-3). Dans ce cas, il retourne immédiatement vrai car un chemin a été trouvé (c'est le chemin détecté entre A- et C- de l'exemple Fig 11 ). Dans le cas contraire, la recherche d'un chemin est appliquée au niveau du graphe tout entier. Pour deux sommets s1 et s2 placés sur deux chaînes chaîne1 et chaîne2, tels que rang(s1) < rang (s2), la recherche consiste d'abord à comparer le rang des sommets extrémités des chaînes chaîne1 et chaîne2 respectivement. Pour la chaîne1, il s'agit du sommet de fin (sA dans l'algorithme) et pour la chaîne2 il s'agit du sommet de début (sB). Dans le cas d'égalité, on vérifie d'abord si les deux sommets ne correspondent pas au même sommet du graphe, auquel cas un chemin existe. Si le rang de sA est supérieur ou égal à celui de sB, il ne peut exister de chemin. Le dernier cas nécessite une recherche exhaustive sur le graphe (fonction Recherche_Chemin). Cette recherche est améliorée dans Madeus par deux mesures :
La démarche adoptée dans Madeus consiste à réduire
ces chaînes de façon à obtenir une seule chaîne
qui représente cette portion du document dans le graphe. L'objectif
est de ramener le processus de vérification au cas quantitatif ou
indéterministe. Afin d'illustrer notre démarche, nous exposons
des exemples de portions de graphes comportant des relations causales.
Les graphes présentés sont constitués de trois chaînes
(une par intervalle) A, B et C de durée [lA, uA],
[lB, uB] et [lC, uC] respectivement.
Ces chaînes sont liées selon les cas illustrés dans
la Fig 14 par les relations Parmin (A, B, C), Parmaster
(Bm, A, C) et Parmax(A, B, C).
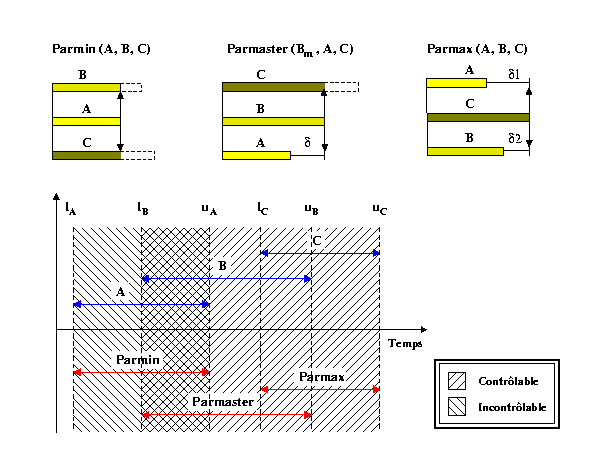
L'illustration graphique de la Fig 14 représente une des dispositions temporelles possibles pour chacune des trois relations en fonction des positions relatives des bornes des chaînes A, B et C. Nous avons en plus supposé l'incontrôlabilité de la chaîne A et la contrôlabilité des chaînes B et C (cf. les hachures dans la Fig 14 ). La difficulté de gérer toutes les dispositions possibles est liée aux deux facteurs suivants :
Pour chaque sommet i, j et k du graphe, Dij représente la contrainte de la chaîne de sommets extrémités i et j :
Dij @ Djk = (i : [a, b] : j) @ (j : [c, d] : k) = (i : [a+c, b+d] : k)
Dij intersect D'ij = (i : [a, b] : j) intersect (i : [c, d] : j) = (i : [max(a, c), min(b, d)] : j)
L'algorithme que nous utilisons dans Madeus est fondé sur une
version incrémentale [CHL 95]
de l'algorithme DPC (Directional Path Consistency)[MEI
92]. Cet algorithme est plus performant que PC-2 [MAC
85]. Grâce au tri topologique du graphe, il permet de détecter
toutes les incohérences quantitatives [MEI
92] en renforçant une forme restreinte de cohérence sur
le graphe : la DPC-Cohérence :
Définition 3 (DPC-Cohérence) : Soit un graphe G = (I, A, E) un réseau de contraintes numériques trié topologiquement. Le réseau G est DPC-cohérent si la condition suivante est satisfaite :
forall i, j, k in I, (rang(i) < rang(k)) vee (rang(j) < rang(k))
Rightarrow Dij subseteq Dik @ Dkj
Avant d'aborder le déroulement détaillé de cet
algorithme, nous commençons d'abord par une illustration graphique
de son principe de fonctionnement, en particulier, par le parcours du graphe
effectué à chaque insertion ou modification d'une chaîne
temporelle.
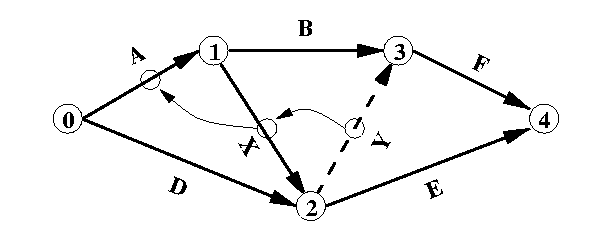
Considérons un graphe composé de sept chaînes A, B, D, E, F, X et Y (voir la Fig 15 ), et soit Y la chaîne qui, après l'insertion d'une relation dans le document, a été modifiée resp. créée dans le graphe et qui doit être vérifiée quantitativement. En prenant en compte l'ordre topologique du graphe, le principe de l'algorithme consiste à vérifier ou renforcer la propriété de DPC-Cohérence en examinant ou modifiant, si c'est possible, la chaîne X. Si celle-ci est modifiée, l'algorithme examine la chaîne A et ainsi de suite à l'échelle du graphe tout entier.
L'algorithme permet de prendre en compte une ou plusieurs chaînes à la fois. Il suffit de l'initialiser avec la/les chaînes en question. Pour toute chaîne Ch à vérifier, on désignera par Ch-et Ch+ les sommets de début resp. de fin de Ch. L'algorithme exploite les aspects suivants du graphe temporel afin de détecter rapidement les incohérences quantitatives :
Booléen <== DPC_incrémental (GCh=(ICh,ACh,ECh), Chaînes_modifiées : C)
{
1. Liste = emptyset ;
2. pour chaque Ch in C {
3. Liste = Liste union {Sommet_de_fin_de_la_chaîne(Ch)}
4. Ch.Modifié = Vrai;
5. }
6. /* liste contient tous les sommets de fin des chaînes
7. modifiées */
8. tant que Liste =/= emptyset {
9. k <== Sommet_de_plus_haut_rang(Liste);
10. Liste <== Liste - {k};
11. Pour chaque arc a1 = (i, j) | rang(j) < rang(k) et
12. a2 = (i, k), a3 = (j, k) in ACh
13. si a2.Modifié ou a3.Modifié alors
14. {
15. Temp <== Dij ;
16. Dij <== Dij intersect ( Dik @ Dkj);
17. ACh <== ACh union {(i, j)};
18. si Dij = emptyset alors retourne (Faux)
19. si Dij =/= Temp alors {
20. /* la chaîne X est modifiée, il faut répercuter ses 21. modifications sur les autres chaînes */
22. List <== List union {j};
23. a1.Modifié = Vrai;
24. }
25. }
26.retourne (Vrai);
}
Cet algorithme utilise une structure de données Liste pour stocker les sommets qui doivent être vérifiés. Ces sommets seront traités selon leur ordre topologique décroissant dans le graphe. Pour cette raison, à chaque fois qu'un nouveau sommet doit être ré-examiné, il est inséré dans la structure Liste en respectant cet ordre. Pour chaque chaîne insérée dans le graphe et qui doit être vérifiée, la Liste est initialisée avec le sommet de fin de cette chaîne. Pour un sommet k, il suffit de considérer des paires de sommets (i, j) tels que l'une des chaînes de i à k ou de j à k a été préalablement modifiée. Les chaînes modifiées sont marquées moyennant un champ (Modifié) qui permettra à l'algorithme d'identifier celles en cours de propagation.
Nous illustrons maintenant le fonctionnement de cet algorithme sur l'exemple
de la Fig 15 avec les valeurs de durées suivantes
A:[3,15], B:[1,6], F:[2,7], D:[6,12] et E:[4,9]. Nous partons d'une configuration
initiale (sans les intervalles X et Y) où ces intervalles sont disposés
sur deux chaînes parallèles C1 et C2, où C1 est composée
de la séquence {A, B, C} et C2 de la séquence {D, E} (voir
Fig 17 ).

Après l'insertion de la relation A before [0,2] E nous obtenons une nouvelle topologie du graphe qui conduit à l'insertion d'un délai. Cette relation se traduit sur le graphe par l'insertion d'un délai X entre le sommet n2 et n3. Cette insertion modifie la configuration des chaînes existantes du graphe en créant une nouvelle chaîne C3 (celle correspondant au délai X), divise la chaîne C1 en deux nouvelles chaînes C1 et C4 (voir Fig 18 ) ainsi que la chaîne C2 en deux nouvelles chaînes C2 et C5. Comme cette relation n'introduit pas d'incohérence qualitative, nous appliquons maintenant l'algorithme de vérification quantitative pour nous assurer de la validité du nouveau scénario.
Après traduction en relations d'instants et insertion dans le
graphe, les chaînes touchées par cette modification sont (C1,
C2, C3, C4, C5) (Fig 18 ). Il suffit alors d'appliquer
l'algorithme en prenant initialement les chaînes en question. Notons
qu'étant donné que la structure Liste contient des sommets,
il suffit d'insérer une seule fois un sommet de fin qui appartient
à plusieurs chaînes modifiées.
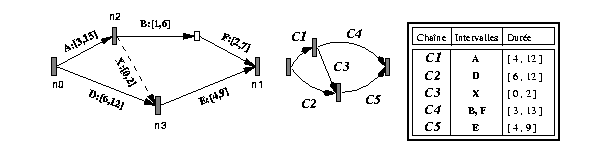
L'application de l'algorithme à l'exemple précédent se déroule alors de la façon suivante (les différents pas sont préfixés par le numéro de ligne de l'algorithme) :
C = {C1, C2, C3, C4, C5}
(5) Liste = {C1+, C2+, C4+}
(9) k = C4+
(10) Liste = {C1+, C2+}
(11) a1 = C3
(15) Temp = [0, 2]
(16) C3.durée = [0, 2] intersect ([3, 13] @ [-9, -4]) = [0, 2] (non modifié)
(9) k = C2+
(10) Liste = {C1+}
(11) a1=C1
(15) Temp = [3, 15]
(16) C1.durée = [3, 15] intersect ([6, 12] @ [-2, 0]) = [4, 12] (modifié)
(23) C1.Modifié = Vrai
(9) k = C1+
(10) Liste = emptyset
(26) L'insertion de la chaîne est donc quantitativement cohérente.
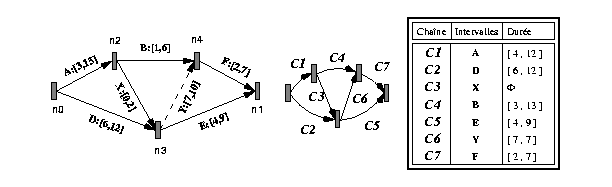
Considérons maintenant l'insertion d'une nouvelle relation : D before [7, 10] F dans le scénario temporel de la Fig 19 . Cette relation se traduit sur le graphe par l'insertion d'un délai Y entre le sommet n3 et n4. Cette insertion modifie la configuration des chaînes existantes du graphe en créant une nouvelle chaîne (celle correspondant au délai Y) et en divisant la chaîne C4 de la Fig 18 en deux nouvelles chaînes C4 et C7 (voir Fig 19 ).
Initialement la liste Liste est composée des sommets de fin de chaînes qui viennent d'être modifiées et de la chaîne créée (celle correspondant au délai Y) :
C = {C4, C5, C6, C7}
(5) Liste = {C4+, C5+}
(9) k = C5+
(10) Liste = { C4+}
(11) a1 = C6
(15) Temp = [7, 10]
(16) C6.durée = [7, 10] intersect ([4, 9] @ [-7, -2]) = [7, 7] (modifié)
(23) C6.modifié = Vrai
(9) k = C4+
(10) Liste = emptyset
(11) a1 = C3
(15) Temp = [0, 2]
(16) C3.durée = [0, 2] intersect ([1, 6] @ [-10, -7]) = emptyset
(18) Cette nouvelle modification est donc quantitativement incohérente.
Dans ce dernier cas, dès que l'algorithme détecte une incohérence, Madeus remet à jour l'état du graphe tel qu'il était initialement (avant ces modifications), ce qui revient à la suppression de la nouvelle chaîne et au reétiquetage des chaînes avec les valeurs qu'elles avaient avant la modification.
Nous avons vu à travers ces exemples le fonctionnement de cet algorithme qui permet la gestion des contraintes numériques d'un scénario temporel. Les avantages qu'il offre sont multiples :
Cette solution, qui peut paraître peu performante, n'est en réalité pas critique. Car l'opération de suppression d'une relation ou d'un élément n'intervient qu'à l'édition, et donc de façon interactive et limitée en nombre, contrairement au processus de construction du graphe (l'insertion d'éléments et de relations) pour des fins de présentation, qui porte sur le document tout entier.
En conclusion, l'algorithme proposé, contrairement à PC-2, permet la vérification quantitative sur le graphe, sans maintenir systématiquement le graphe minimal de contraintes. Cela permet de détecter plus rapidement les incohérences quantitatives. De plus l'algorithme peut être appliqué sur la totalité du graphe, au moment de son chargement initial, tout en gardant de bonnes performances [MEI 92]; il est donc aussi bien adapté à l'édition qu'à la présentation.
L'objectif de la vérification de cohérence indéterministe est d'assurer statiquement que le scénario trouvera une solution à l'exécution. Dans ce qui suit, nous allons simplement décrire de façon informelle la nature des vérifications que nous effectuons dans quelques cas bien identifiés. Une solution plus globale à ce problème n'a pas encore été apportée et nécessite des études plus poussées [VID 97].
Alors que les dates de fin des intervalles contrôlable sont prévisibles, celles des intervalles incontrôlables ne le sont pas et la durée de ce type d'intervalles ne peut donc être déterminée qu'à l'instant même où l'événement de fin se produit : ces instants définissent ainsi des points d'observation privilégiés à partir desquels il va falloir mesurer l'impact sur le scénario en cours d'exécution, en particulier sur les contraintes numériques qu'il contient.
Cas 1
Le premier cas correspond aux situations dans lesquelles la présence
d'un intervalle incontrôlable n'est pas gênante : cet intervalle
n'affecte pas les autres contraintes spécifiées par l'auteur.
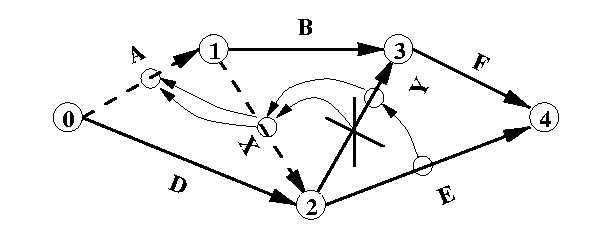
Un tel cas est illustré dans la Fig 22 .
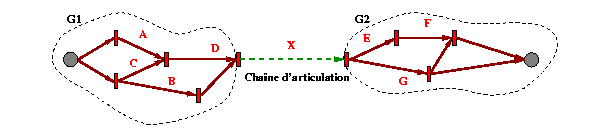
Dans cet exemple, le graphe peut être subdivisé en deux sous-graphes G1 et G2 qui ne sont reliés que par une chaîne contenant l'intervalle indéterministe (Chaîne d'articulation). Ce genre de cas se présente dans des scénarios où, par exemple, le passage entre deux parties est effectué par l'activation d'un élément de type bouton, de durée incontrôlable. Dans une telle configuration, il est clair que quelle que soit la valeur effective de durée prise par cet intervalle la cohérence du graphe n'est pas remise en question.
Cas 2
Le deuxième cas correspond à des situations dans lesquelles
l'intervalle incontrôlable se trouve sur une chaîne dont l'extrémité
droite correspond à un point d'articulation. Autrement dit, cet
intervalle ne remet pas en cause les autres contraintes spécifiées
par l'auteur, à l'exception des contraintes de coïncidence
temporelle, telles que celles des chaînes B et D avec la chaîne
incontrôlable X dans la Fig 23 .
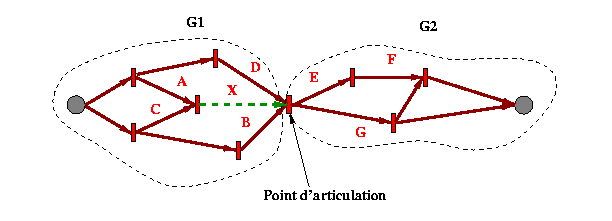
Dans cet exemple, le graphe peut être subdivisé en deux sous-graphes G1 et G2 qui ne sont reliés que par l'instant de fin de la chaîne contenant l'intervalle indéterministe X (le point d'articulation est X+). Ce type de situation ne peut être cohérent que si les chaînes B et D sont flexibles par la fin, comme le sont des éléments discrets (image ou texte). Dans ce cas, la terminaison de la chaîne X « provoque » la terminaison des deux autres chaînes contenant B et D. Nous nous ramenons donc au cas 1 moyennant cette simple vérification.
Cas 3
Le dernier cas consiste à vérifier, pour chaque instant
permettant d'observer la durée d'un intervalle indéterministe,
s'il est possible de le compenser. La compensation est reposée sur
l'utilisation de la flexibilité des éléments contrôlables
dont les instants de début ou de fin se trouvent dans le futur par
rapport à cet instant. Ces instants sont appelés les points
de recouvrement. Soit par exemple une chaîne constituée
de deux intervalles A et B (voir Fig 24 -a). A est
un intervalle incontrôlable A = [lA, uA]i
et omega = (uA- lA) représente son
montant d'indéterminisme. B est un intervalle contrôlable
B = [lB, uB]c et delta = (uB-
lB) représente son montant de flexibilité.
Si la condition delta >= omega est satisfaite, alors l'indéterminisme
peut être compensé dynamiquement de façon à
rendre toute la chaîne contrôlable. Il suffit dans ce cas d'utiliser
la flexibilité delta de façon à rendre la durée
de l'intervalle A constante et égale à uA,
ce qui a pour effet d'« éliminer » l'effet de cet indéterminisme.
On obtient ainsi une chaîne ayant un comportement contrôlable
vis-à-vis du reste du graphe et de durée totale [uA+lB,
uA+uB]i. La cohérence quantitative
de cette chaîne dans le graphe sera donc équivalente à
sa contrôlabilité.
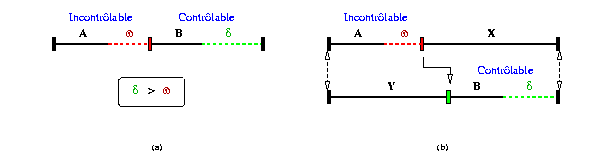
Si l'intervalle incontrôlable ne peut être compensé au niveau de sa chaîne [LAY 96a], la démarche proposée dans Madeus consiste à vérifier si une exploitation de la flexibilité dans les chaînes concurrentes peut permettre de réajuster le scénario. Par exemple, dans le scénario de la Fig 24 -b, deux chaînes parallèles {A, X} et {Y, B} doivent être de durées égales. Pour vérifier que cette contrainte peut être satisfaite, il suffit de s'assurer que les instants de début et de fin de chaînes ont lieu à la même date. Là encore, il est facile de voir que si la flexibilité delta de la chaîne concurrente {Y, B} est supérieure à l'indéterminsme omega de la chaîne {A, X} (condition 1), et si la date de l'instant d'observation A+ a lieu avant le point de recouvrement B-, alors la simultanéité des instants B+ et X+ peut être assurée. Cette portion du graphe est donc contrôlable. La méthode proposée entraîne, pour le graphe de contraintes, l'adjonction d'une durée indéterministe omega sur l'élément englobant. Elle entraîne aussi la suppression de la flexibilité utilisée des chaînes concurrentes. Dans l'exemple de la Fig 21 , cela se traduit par un allongement potentiel de toutes les chaînes concurrentes d'une durée omega, ce qui revient à décaler la partie G2 du graphe (c'est le sous graphe qui représente le futur par rapport à l'instant de fin de la chaîne indéterministe).
Le processus de vérification proposé dans cette section ne couvre pas tous les cas. L'approche adoptée dans Madeus se limite à vérifier localement la possibilité de « réparer » le scénario à partir de l'instant de fin des intervalles incontrôlables, puisque les garanties qu'on souhaite offrir à l'auteur au moment de l'édition, en terme de contrôlabilité, correspondent à celles que nous pouvons effectivement tenir au moment de la présentation [LAY 96a].
La vérification de la contrôlabilité est un problème fondamental qui reste encore aujourd'hui un sujet de recherche ouvert. Des méthodes « préventives » ont fait l'objet d'une étude dans le cadre de la planification robotique [VID 95b][VID 95a][DUB 93]. Cette étude s'oriente maintenant vers des méthodes de recherches exhaustives similaires à celles employées dans le domaine du temps réel [VID 97].
Dans cette section, nous présentons donc deux étapes qui permettent d'aboutir à un document temporellement formaté : l'algorithme qui permet de calculer le réseau de contraintes minimal, et le processus de calcul d'une solution définitive, c'est-à-dire le formatage.
L'algorithme du plus court chemin (all pairs shortest paths) présenté dans le Chapitre III permet de calculer le graphe minimal. Cet algorithme, de complexité cubique O(n3) en temps et en espace, est général car il ne tient pas compte de l'existence d'un ordre topologique entre les sommets. Or le graphe utilisé dans Madeus, étant topologiquement trié, admet une solution beaucoup plus efficace. C'est un algorithme basé sur ce tri que nous proposons ici.
Pour pouvoir appliquer cet algorithme, le graphe d'instants G est utilisé comme un graphe de distance Gd . La contrainte minimale entre deux instants i et j, introduite pour le graphe de distance Gd présenté dans la Chapitre III, est définie par l'intervalle [l, u], où -l représente la longueur du plus court chemin entre j et i, et u représente la longueur du plus court chemin de i à j.
L'algorithme présenté dans la Fig 25
est une variante de l'algorithme de Bellman-Ford [MEI
92][KHA 79] basé sur l'ordre
topologique du graphe. Pour deux sommets i et j du graphe tels que rang(i)
< rang(j), l'ordre topologique permet de limiter la portée du
calcul des plus courts chemins en propageant d'abord le calcul du sommet
i en direction du sommet j. Cela permet de définir la borne de durée
minimale entre i et j. On procède ensuite dans l'ordre inverse pour
déterminer la borne de durée maximale.
(Entier, Entier) <== Plus_court_chemin(GCh = (ICh, ACh, ECh), i, j)
{
1. Pour chaque x in ICh {
2. x.Distance = infty
3. }
4. i.Distance = 0;
5. Pour chaque y in ICh | 0 <= rang(i) <= rang(y) pris dans l'ordre topologique croissant
6. Pour chaque chaîne C = (x, y) in ACh et Dxy = [l, u]
7. y.Distance = min(y.Distance, x.Distance +u)
8. Pour chaque x in ICh | 0 <= rang(x) <= rang(j) pris dans l'ordre topologique décroissant
9. Pour chaque chaîne C = (x, y) in ACh et Dxy = [l, u]
10. x.Distance = min(x.Distance, y.Distance - l)
11. retourne (i.Distance, j.Distance)
}
Pour calculer le graphe minimal correspondant à un élément
composé du document, il suffit d'appliquer l'algorithme deux fois
: une fois entre son instant de début (sommet source) et son instant
de fin (sommet puit), et une nouvelle fois entre son instant de fin et
son instant de début. Cela permet en plus de déterminer les
bornes de durée de toutes les chaînes qu'il contient. L'exemple
de la Fig 26 reprend un état cohérent
du graphe présenté en 3.2.3. et qui
correspond dans ce cas à un élément composé
X. L'application de l'algorithme sur ce graphe permet d'aboutir au graphe
minimal représenté en Fig 26 .
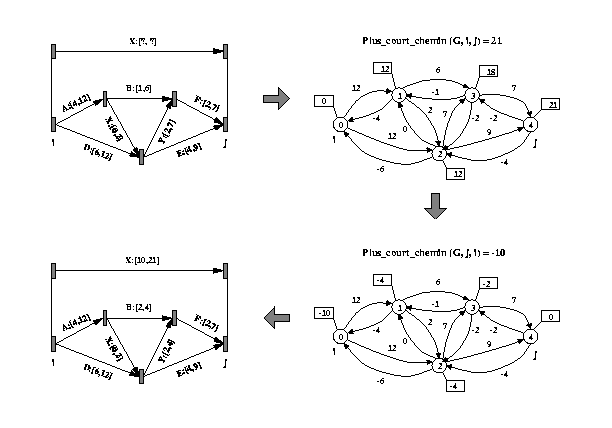
La complexité de cet algorithme est linéaire par rapport au nombre de sommets n et d'arcs e contenus dans le graphe : O(n+e). Il est donc beaucoup plus rapide que l'algorithme all pairs shortest paths présenté dans le Chapitre III ainsi que ses variantes comme [KHA 79]. Donc, si on considère le coût de la vérification de cohérence quantitative cumulé au coût de calcul du graphe minimal, nous obtenons une complexité totale linéaire en fonction du nombre de sommets n et du nombre d'arcs e : 2 * O(n+e) + O(n k2) cong O(n+e).
Chaque phase de l'algorithme consiste à dater les différents
sommets du graphe en partant de son sommet source, respectivement puits.
Dans la première phase, cette datation est effectuée dans
l'ordre topologique croissant (lignes 1-22 de l'algorithme de la Fig
28 ) et permet de définir une valeur de durée (C.durée1)
pour chaque chaîne. La deuxième phase est effectuée
dans l'ordre décroissant et permet de définir la valeur C.durée2.
La Fig 27 représente l'application de cet
algorithme à l'exemple de la Fig 26 .
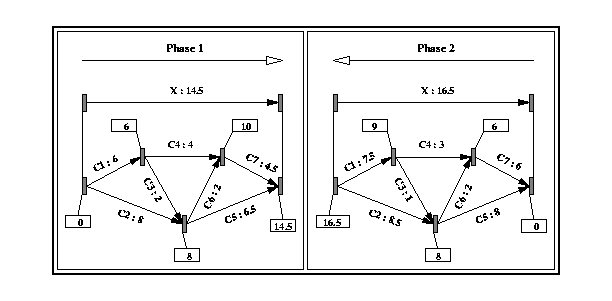
L'algorithme prend en compte les durées préférables des différentes chaînes (lignes 8, 12 et 16). De plus, à chaque étape du calcul de la date d'un sommet du graphe, l'algorithme s'assure que la date retenue respecte bien les contraintes de chacune des chaînes (lignes 13, 14, et 17).
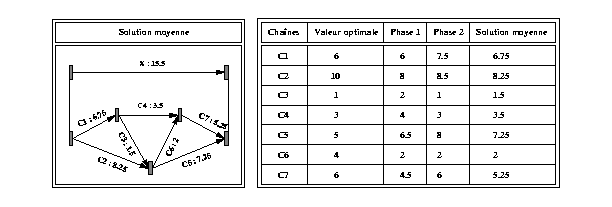
La solution finale est alors obtenue par la valeur moyenne des valeurs
issues du calcul de chaque phase. Cette nouvelle moyenne constitue elle-même
une solution car les contraintes du graphe forment un système linéaire.
Formater (GCh=(ICh, ACh, ECh))
{
1. Liste = I - { source };
2. Distance(source) = 0;
3. Tant que Liste =/= emptyset {
4. n <== Sommet_de_rang_Minimum(Liste);
5. Liste <== Liste - { n }
6. Si (Degré_Entrant(n) == 1) {
7. Pour la chaîne C | C+ = n
8. Distance(n) = Distance(C-) + C.optimale;
9. } sinon {
10. somme = 0; min_Max = infty ; max_Min = 0 ;
11. Pour chaque chaîne C =[l, u] | C+ = n {
12. somme = somme + Distance(C-) + C.optimale;
13. min_Max = min( min_Max, Distance(C-) + u);
14. max_Min = max( max_Min, Distance(C-) + l);
15. }
16. Moyenne = somme / Degré_Entrant (n);
17 Moyenne = min ( min_Max, max (Max_min, Moyenne));
18. Pour chaque chaîne C | C+ = n {
19. C.durée = Moyenne - Distance(C-);
20. }
21. Distance (n) = Moyenne;
22. }
23. /* calcul de C.durée2 par datation dans l'ordre topologique décroissant */
24. ...
25.. Pour chaque chaîne C {
26. C.effective = (C.durée1 + C.durée2 )/2
27. }
}
L'algorithme de la Fig 28 permet le formatage d'un document en temps linéaire : O(n).
Les valeurs obtenues sont ensuite propagées à l'échelle
des chaînes aux éléments multimédia qu'elles
contiennent. Ce calcul de valeurs tient compte du type de média
de chaque élément. Par exemple, si on considère une
chaîne formée simplement par un élément vidéo
suivi d'un délai temporel, on commence en priorité par le
calcul de la durée de l'élément vidéo aux dépens
de l'élément délai. Dans Madeus, cette notion est
étendue à l'ensemble des média en attribuant à
chacun un ordre de priorités. Ces priorités sont définies
dans l'ordre suivant : Audio, Vidéo, Animations, Texte, Délais.
On privilégie ainsi les éléments continus, ensuite
les éléments discrets et enfin les éléments
vides de contenu : les délais. Après cette phase, le document
est sous sa forme exécutable et l'information portée par
le graphe peut directement être exploitée dans le processus
de présentation.
L'établissement d'une politique automatique de répartition des contraintes entre les différents média reste une opération délicate [BUC 93][HAM 93][KIM 95]. Car elle peut engendrer des situations qui ne correspondent pas nécessairement aux souhaits de l'auteur. Ce problème n'est cependant pas nouveau dans le domaine des documents; il peut être comparé au comportement des formateurs spatiaux de texte comme LaTex [LAM 86] et Thot [QUI 86].
Signalons finalement qu'une partie du formatage est effectué dynamiquement, à l'exécution. Car la prise en compte des durées effectives des intervalles incontrôlable nécessite un processus réactif de réajustement du graphe (cf. 3.2.4). Ceci ne remet pas en cause l'opération de formatage, car c'est à partir des durées calculées durant cette phase que le réajustement du graphe pendant la phase de présentation est réalisée (voir le section 3.2).
| Document | UR | Inria | Scène | Hubble | Ancres |
|---|---|---|---|---|---|
| Nombre d'éléments | 167 | 98 | 42 | 21 | 11 |
| Nombre de relations | 137 | 93 | 36 | 20 | 8 |
| Nombre de sommets | 189 | 110 | 52 | 33 | 12 |
| Nombre d'arcs | 271 | 155 | 80 | 43 | 18 |
| Nombre de chaînes | 137 | 70 | 57 | 23 | 13 |
| Niveaux hiérarchiques | 6 | 4 | 3 | 2 | 2 |
| Temp CPU (ms) | 114.52 | 69.54 | 30.87 | 15.46 | 7.6 |
Les algorithmes sont écrits en langage C et les mesures sont effectuées sur une machine Sun-Ultra-Sparc (sous le système Unix Solaris 2.5). Chaque mesure a été effectuée 500 fois au cours du fonctionnement normal de l'application et du système. Ces chiffres témoignent d'une dépendance quasi-linéaire entre la taille du document en terme de nombre d'éléments et son temps de traitement. Ces dépendances s'expliquent surtout par le fait que le nombre de chaînes parallèles à un instant donné de la présentation n'excède pas la dizaine.
Le graphe extrait de la représentation peut ainsi être directement utilisé pour ordonnancer le document. C'est cette phase que nous décrivons dans le chapitre suivant.
Dans les systèmes de documents multimédia l'opértion
de recherche de solution est aussi appellé formatage.
(2)
Nous utiliserons dans la suite les termes graphes ou hypergraphe pour désigner la structure du problème de synchronisation temporelle.