Chapitre 3
Modèles temporels pour les documents multimédia
[Table des matières]
1 Introduction
Dans le chapitre précédent, nous avons montré le rôle
important du temps à travers son impact aussi bien sur l'architecture
d'une application d'édition et de présentation multimédia,
que dans un modèle de documents. Nous avons souligné en particulier
que le problème de la synchronisation temporelle s'étend
depuis le niveau spécification jusqu'aux autres niveaux liés
à la présentation. Pour apporter des réponses adaptées
à chacun de ces niveaux, il est nécessaire d'adopter une
analyse descendante des différents problèmes. En effet, l'opération
d'édition qui consiste à spécifier la synchronisation
temporelle d'un document multimédia constitue le point de départ
de son cycle de vie. Pour un auteur, ce cycle comprenant la création,
la préparation, la correction et la publication est similaire à
celui rencontré par un développeur dans le domaine du génie
logiciel. La réutilisation maximale, la puissance des fonctions
d'édition et la facilité de maintenance des documents et
de leurs composants sont des qualités très recherchées.
Un système d'édition doit en outre gérer une description
précise et cohérente de l'information temporelle. Une telle
description conditionne, en effet, la restitution correcte du document
à l'utilisateur (étape de présentation).
Cependant, on peut constater que l'on dispose de peu d'expérience
en matière de composition temporelle (domaine neuf du fait de la
technologie) et, de fait, les travaux pour la spécification de documents
multimédia sont encore peu nombreux. Ce facteur, conjugué
à la grande richesse temporelle des éléments et de
leur schéma de composition temporel, rend actuellement l'opération
d'édition particulièrement complexe. La réduction
de cette complexité passe par la définition d'un niveau d'abstraction
suffisant pour rendre cette opération plus accessible.
C'est dans cette perspective qu'on se propose, dans ce chapitre, d'étudier
les modèles temporels pour les documents multimédia.
Un modèle temporel pour l'édition et la présentation
multimédia est composé de trois parties [PER
96]:
-
Un langage temporel qui permet la spécification d'un scénario.
-
Des mécanismes d'analyse qui permettent de prévenir
les incohérences ou de les détecter à l'édition,
par exemple, lorsque l'auteur introduit une relation temporelle entre deux
éléments qui, compte tenu de leurs valeurs de durée,
ne peut être satisfaite.
-
Des mécanismes de synthèse qui permettent statiquement
ou dynamiquement de produire une présentation conforme aux spécifications
de l'auteur. Généralement le module du système d'édition
qui assure cette fonction est appelé formateur temporel par
analogie aux formateurs de texte comme Latex [LAM
86] ou Thot [QUI 86].
La première partie de ce chapitre est consacrée à
la définition d'un scénario temporel, à la représentation
de l'information temporelle de base et à la spécification
de la synchronisation d'un document. Dans la deuxième partie, on
aborde les techniques d'analyse et de synthèse des spécifications
de scénarios. Cette analyse porte principalement sur le processus
de composition temporelle, la vérification de la cohérence
et la production automatique d'une représentation de plus bas niveau
adaptée à la phase de présentation.
[Table des matières]
2 Scénarios temporels
Dans cette section, nous présentons la notion de scénario
temporel, les différentes façons de les décrire, ainsi
que les qualités attendues d'un modèle temporel adapté
à l'édition de documents multimédia.
[Table des matières]
2.1 Définitions
Un scénario temporel définit comment les éléments
d'un document s'enchaînent dans le temps. C'est en quelque sorte
la projection du document sur la dimension temporelle.
À titre d'exemple, un document reproduisant un exposé
est composé d'un ensemble de transparents qui sont enchaînés
en séquence. Supposons que chaque transparent soit composé
d'un texte, d'une image et d'un commentaire audio et que le temps de présentation
du transparent soit égal à la durée du commentaire
audio. Les trois entités sont donc reliées entre elles dans
le temps (elles démarrent et finissent en même temps) et elles
sont dépendantes du temps (le commentaire audio dure par exemple
2 minutes).
À tout scénario, peuvent correspondre une ou plusieurs
traces d'exécution qui le respectent. Une trace d'exécution
est définie de la façon suivante : c'est une suite de triplets
(instant, ensemble d'observations, séquence d'actions). Chaque
action correspond au démarrage d'un élément et une
observation à une terminaison.
On peut distinguer deux types de scénarios temporels dans une
présentation multimédia :
-
Scénarios déterministes : ils correspondent à
des enchaînements entièrement définis avant la présentation
d'un document. On peut calculer statiquement une date de début et
une date de fin pour tous les éléments. Cela suppose en particulier
qu'on connaisse la durée de tous les éléments. La
trace d'un scénario déterministe est unique.
-
Scénarios indéterministes : ils correspondent à
des enchaînements qui sont définis en fonction de données
connues uniquement au moment de la présentation (occurrence d'une
interaction utilisateur). Un scénario indéterministe est
caractérisé par l'existence d'un ensemble de traces qui lui
correspondent.
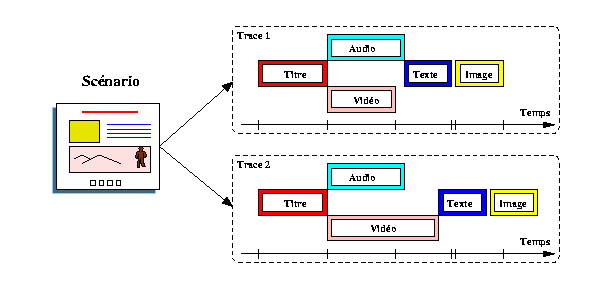Fig 0. Exemple de scénario temporel indéterministe
Dans la figure Fig 0 , nous décrivons en
langage naturel un exemple de scénario de type indéterministe.
Dans cet exemple, une présentation est composée de cinq éléments
multimédia dont les dépendances temporelles sont les suivantes
: un élément de type texte (Titre) est présenté
durant 40 secondes. Il est suivi d'une séquence Audio et d'une séquence
Vidéo. Ces deux séquences démarrent simultanément.
Lorsque les deux sont terminées, un élément Texte
est présenté pendant 30 secondes suivi d'une Image. On suppose
que les éléments Audio et Vidéo sont stockés
sur un site distant et qu'il n'existe aucune connaissance a priori
sur leur durée de présentation qui peut varier d'une exécution
à l'autre. Chaque exécution du scénario conduit à
une trace différente (voir Fig 0 ). Nous constatons
donc qu'à partir d'une même description en langage naturel,
les traces peuvent varier d'une présentation à l'autre.
De façon analogue à l'exemple présenté,
une méthode de spécification d'un scénario doit être
suffisamment générale pour couvrir l'ensemble de ses traces.
Bien entendu, cette description doit s'appliquer aussi bien aux scénarios
déterministes qu'aux scénarios indéterministes.
[Table des matières]
2.2 Niveau de représentation des scénarios
Un scénario peut être spécifié de deux façons.
La première consiste à décrire un scénario
à travers une trace particulière, c'est le principe des timelines.
Cela revient à le considérer comme un ensemble d'instants
indépendants qui se rapportent à un repère temporel
unique (le début du document). Dans ce type de représentation,
basé sur un temps absolu, les relations temporelles entre les événements
sont implicites et l'ordre induit est total. L'analyse et la synthèse
sont dans ce cas inutiles, et la représentation du document peut
être exploitée telle quelle pour ordonnancer la présentation.
En effet, il suffit simplement de déclencher les différents
événements à leur date de début. Ce type de
représentation ne permet pas de représenter des scénarios
indéterministes. De plus, il n'est pas adapté à la
nature incrémentale du processus d'édition. En effet, toute
modification nécessite une reconsidération globale de la
spécification, du fait de l'incapacité de ce type de représentation
à expliciter les relations temporelles. Ce sont ces caractéristiques
qui nous la font qualifier de représentation de bas niveau.
À l'opposé, la seconde façon consiste à
décrire le scénario à partir d'une mise en relation
des différents éléments qui le composent. Cette forme
de temps relative, contrairement à la précédente,
permet de rendre explicite toutes les dépendances temporelles du
scénario et induit un ordre partiel entre ses différents
instants. Cette représentation de haut niveau permet d'obtenir
des structures temporelles abstraites plus facile à organiser et
à mettre à jour. Cependant, ces qualités ne sont pas
acquises sans contre-partie. La nature de la représentation du temps
utilisée introduit dans les spécifications de scénarios
des risques d'incohérences. De plus, pour effectuer la présentation,
il est nécessaire de rapporter cette représentation au temps,
d'où l'importance de fournir des mécanismes d'analyse et
de synthèse pour ce type de représentation.
[Table des matières]
2.3 Critères d'évaluation d'un modèle temporel
Avant d'aborder plus en détail les modèles temporels, il
convient de préciser d'abord les critères qui permettent
d'évaluer un modèle donné. Dans notre étude,
l'objectif attendu de la modèlisation est double. Il s'agit d'une
part de faciliter l'opération d'édition d'un document et
donc de satisfaire au mieux les exigences d'un auteur, et d'autre part
de produire automatiquement une forme du document adaptée à
la présentation. Un modèle donné doit répondre
aux objectifs concernant la dimension temporelle des documents multimédia.
Ils se résument ainsi :
-
Puissance expressive : le langage temporel offert par le modèle
doit permettre la spécification de schémas de synchronisation
arbitrairement complexes. Une évaluation de l'expressivité
peut se ramener à une mesure du "nombre" de schémas de synchronisation
exprimables [BLA 96].
-
Structuration de l'information temporelle : l'organisation logique
d'un document, permettant la modularité et l'encapsulation de ses
parties, doit être prise en compte dans les spécifications
temporelles.
-
Vérification de la cohérence temporelle : le modèle
temporel doit être doté de mécanismes permettant de
détecter et d'indiquer à l'auteur les incohérences
d'un schéma de synchronisation donné.
-
Intégration de données multimédia hétérogènes
: la représentation et le traitement des éléments
multimédia de base doivent être homogènes pour faciliter
l'opération de composition.
-
Adaptation à la nature incrémentale du processus d'édition
: la création d'un document se fait généralement
par une modification progressive de son contenu et de sa structure temporelle.
L'incrémentalité, qui consiste à prendre en compte
les opérations d'édition une par une, doit être supportée
au niveau temporel.
-
Performance des mécanismes d'analyse et de synthèse :
Un environnement d'édition / présentation de documents multimédia
est un environnement interactif, d'où la nécessité
d'apporter une attention particulière aux performances des techniques
employées [DEC 91].
À travers les modèles temporels, on cherche ainsi à
retrouver deux composants importants de l'édition multimédia
: le premier est un langage temporel permettant l'expression de la synchronisation
et le second est l'ensemble des méthodes pour son analyse et sa
synthèse. Les critères introduits doivent être évalués
au niveau du modèle pour juger si celui-ci est adapté à
l'édition multimédia.
[Table des matières]
3 Représentation de l'information temporelle multimédia
Dans le chapitre précédent, nous avons clairement identifié
deux phases de traitement d'un document multimédia : son édition
et sa présentation. Dans ces deux phases la dimension temporelle
apparaît au coeur du problème et nécessite donc une
étude plus approfondie.
De la même façon que les dimensions logique [HYT
92][ISO 92] et spatiale [ROI
94] des documents ont été modélisées, nous
proposons dans cette section un modèle temporel permettant de caractériser
les présentations multimédia ainsi que le processus de leur
mise en relations dans un document : la composition temporelle.
[Table des matières]
3.1 Modélisation de l'information temporelle de base
Avant d'aborder les méthodes de spécification d'un scénario,
nous commençons par la définition des entités de base
qui le composent. En particulier, nous caractérisons le comportement
temporel de chaque élément indépendamment d'un scénario
donné. Cette étape nous permet de modéliser les différents
éléments multimédia de façon homogène
et indépendante de leur contenu et de leur type (audio, vidéo,
texte, etc.), on parle alors d'unités temporelles.
Tout élément multimédia peut être manipulé
à travers trois informations temporelles essentielles :
-
Son instant de début.
-
Sa durée de présentation.
-
Son instant de fin.
L'une de ces trois informations est redondante. En effet, il est possible
de calculer l'une en fonction des deux autres. Mais le choix des informations
retenues fait partie du langage et donc du modèle, car la mise en
relation des éléments se fait à partir de ces informations.
Il existe deux façons de représenter le déroulement
d'un scénario : à travers les changements qui surviennent
(la terminaison de la vidéo correspond au démarrage de l'audio)
ou au contraire en reliant globalement les activités entre elles
(la séquence audio est présenté pendant la séquence
vidéo). Ceci débouche sur deux types de représentations
:
-
Une représentation fondée sur les instants. Dans ce
cas, un élément multimédia, qu'il soit logique ou
de base, est décrit dans un scénario par un instant de début
et un instant de finnote1, comme dans Firefly
[BUC 93] et Maestro [DRA
93].
-
Une représentation fondée sur les intervalles. Un
élément multimédia est considéré comme
une entité temporelle de base décrite par sa durée
comme dans OCPN [LIT 93] et Cmifed
[BUL 95].
Dans les représentations multimédia fondées sur les
intervalles, les unités temporelles de base peuvent être classées
en trois catégories en fonctions des caractéristiques attachées
à leurs durées :
-
Les intervalles discrets. Ce sont des unités dont la présentation
ne dépend pas du temps, comme le texte ou les images fixes. En vue
de leur intégration avec d'autres données ayant une dimension
temporelle, celles-ci peuvent être affectées d'une durée
de présentation explicite ou implicite dans le contexte d'un scénario
donné.
-
Les intervalles déterministes continus. Ils correspondent
à des données dont la présentation dépend du
temps et dont la valeur de durée est connue a priori. Des
flots audio et vidéo sont des exemples de telles unités temporelles.
Dans certains cas comme la vidéo, la durée effective de présentation
de ces données est liée à la vitesse de restitution
des images qui la composent.
-
Les intervalles indéterministes (discrets ou continus). Ces
intervalles se distinguent par le fait qu'ils n'ont pas de durée
connue a priori. Ils correspondent, par exemple, à des flots
audio ou vidéo continus auxquels on accède à travers
le réseau. Ce sont, en partie, ces éléments qui engendrent
des scénarios indéterministes.
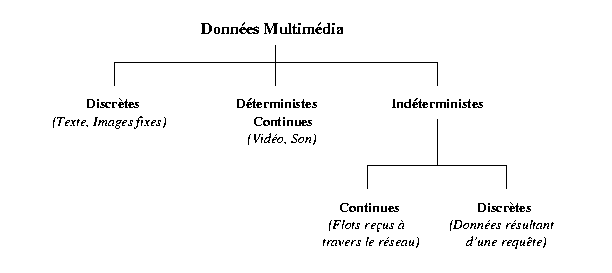Fig 1. Les unités temporelles de base
Domaine de validité d'un intervalle
Les unités de présentation à base d'intervalles
peuvent être modélisées par un ensemble décrivant
leur valeurs possibles de durée ; on parle de leur domaine de validité
ou de leurs bornes. Le domaine de validité d'une unité de
présentation peut être défini par un triplet de valeurs
[min, nom, max] :
-
La durée minimale min représente la borne inférieure
acceptable (au regard de la qualité de restitution) pour la durée
de présentation d'un élément multimédia. La
date de l'instant de fin correspondant à cette durée est
appelée date au plus tôt.
-
La durée nominale nom correspond aux contraintes de synchronisation
intrinsèques d'un élément.
-
La durée maximale max représente la borne supérieure
acceptable pour la durée de présentation d'un élément
multimédia. La date de l'instant de fin correspondant à cette
durée est appelée date au plus tard.
Le comportement temporel de l'ensemble des éléments multimédia
peut être représenté par ces domaines de validité.
Si on se restreint à la manipulation des éléments
à travers ces domaines, il devient possible d'abstraire leur contenu
au sein du modèle et de rendre homogène leur représentation
et leurs traitements. Les contraintes liées à la perception
humaine de la synchronisation se traduisent alors simplement par un choix
adapté de ces trois valeurs.
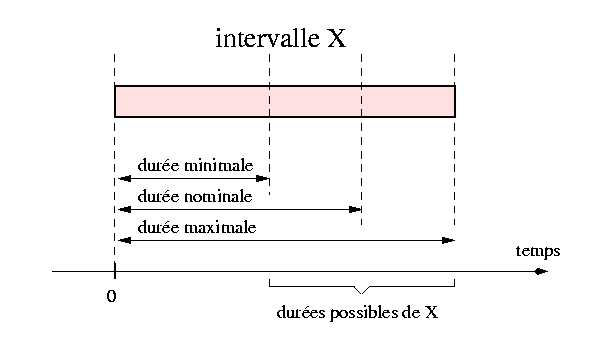Fig 2. Domaine de validité d'un intervalle temporel
On peut noter qu'il existe des différences dans le sens attaché
à ces bornes en fonction des catégories introduites plus
haut (continus, discrètes, indéterministes) [ERF
93]. Ces différences peuvent se traduire par l'amoindrissement
du sens de l'une des valeurs du triplet. C'est le cas des unités
temporelles de type continu où le domaine de validité correspond
à une notion de flexibilité temporelle inhérente
à certains éléments multimédia. Par exemple,
pour un élément de type animation représenté
par les bornes [20, -, 30] secondes, l'auteur peut choisir à sa
guise la valeur qui lui convient dans cette plage car il s'agit de contraintes
temporelles synthétiques. Pour les éléments discrets
comme le texte, cette flexibilité est infinie (bornes ]0, -,infty]),
et se distingue comme le cas de l'animation par l'absence de valeur optimale.
Le domaine de validité constitue donc un paramètre d'édition
puisqu'il est sujet à un choix d'une part pour la définition
des valeurs admissibles et d'autre part pour la valeur définitive
retenue pour un scénario donné. Dans certains cas comme pour
la vidéo et l'audio, le domaine de validité peut être
lié à une notion de solution préférable
mesurée en fonction de l'écartement par rapport à
la valeur nominale (qui correspond aux contraintes naturelles). Par exemple,
pour un élément de type audio modélisé [23,
25, 27], une durée de 26 sera jugée plus souhaitable que
la valeur maximale de 27, bien que cette dernière reste acceptable.
Intuitivement, ce dernier type d'éléments introduit plus
de contraintes puisque le choix des valeurs de validité est généralement
plus restreint que dans les exemples de l'animation et du texte.
La mise en relation d'éléments est la seconde source de
contraintes. Par exemple dans un scénario dans lequel une animation
est présentée en même temps qu'un élément
audio, les domaines de validité doivent être combinés
pour retenir celui qui convient le mieux.
[Table des matières]
3.2 Expression des relations temporelles
Les relations temporelles permettent de décrire la façon
dont les éléments multimédia doivent être combinés
temporellement pour produire le scénario d'un document. Les relations
temporelles servent à la fois comme entrée de la partie analyse
d'un modèle et comme une mémoire des intentions de l'auteur.
Cette représentation permet de définir l'état courant
d'un document sur lequel s'appliquent les différentes opérations
de composition.
Afin de définir un jeu de relations ou d'opérateurs temporels
permettant la construction d'un document, nous étudions dans cette
section trois aspects importants liés à ces relations temporelles
qui peuvent intervenir pour décrire un scénario :
-
Les unités temporelles mises en jeu dans les relations.
-
La sémantique temporelle associée à ces relations.
-
La topologie de la structure temporelle du scénario (arbre, graphe).
Étant donnée l'existence de deux modes de représentation
des unités temporelles (les instants et les intervalles), il en
résulte deux classes de relations temporelles. Les relations temporelles
fondées sur les instants et les relations fondées sur les
intervalles.
Dans ces deux types de relations, les scénarios sont représentés
à partir d'un ensemble B de relations temporelles dites primitives.
Ces relations sont exclusives et permettent d'exprimer comment les unités
temporelles d'un document (les éléments) se situent les unes
par rapport aux autres.
[Table des matières]
3.2.1 Relations à base d'instants
Dans les relations à base d'instants (algèbre d'instantsnote2
notée PA : Point Algebra), les unités temporelles
considérées dans les relations sont les instants de début
et de fin des éléments. Étant donnés deux instants
dans un scénario, trois relations peuvent exister entre eux. Un
instant peut en précéder un autre (<), lui succéder
(>) ou lui être égal (=). L'ensemble des relations primitives
de l'algèbre d'instant est noté B = { <, >, = }.
Dans certains cas, les relations entre certains instants d'un scénario
peuvent être connues de façon moins précise. Dans l'opération
d'édition, il existe deux sources à ce genre d'imprécision
:
-
Le scénario est en cours de construction et l'auteur n'a pas encore
placé de façon définitive les éléments
les uns par rapport aux autres.
-
Des intervalles indéterministes sont présents dans le scénario,
ayant comme conséquence le positionnement temporel imprécis
entre certains éléments.
Afin d'illustrer le premier type de situations, supposons que la seule
relation que nous connaissions entre deux instants e1 et e2
est que e1 ne peut avoir lieu après e2. Cela signifie
que e1 a lieu avant ou en même temps que e2. Cette
relation est notée e1< e2 wedge e1 = e2
ou encore e1 {<, = } e2.
L'ensemble des relations composées ou disjonctives, noté
2B, représente des disjonctions des relations
primitives. Puisqu'il existe 3 relations primitives, il en résulte
23 = 8 relations composées qui forment les parties de
B. Dans la suite, chacune de ces relations sera notée par
un symbole particulier. Par exemple, au lieu de noter e1 {<,
=} e2, nous utiliserons e1 <= e2. Les relations
composées à base d'instants sont : bot, <=, <, =, >,
>=, =/=, ?, où la relation ? représente une disjonction contenant
l'ensemble des relations primitives et bot l'ensemble vide des relationsnote3.
De façon intuitive les relations primitives <, >, = sont utiles
pour la composition multimédia car elles interviennent dans la construction
des scénarios multimédia les plus simples. En est-il de même
pour toutes les formes disjonctives {<=, >=, =/=, ?} ? Afin de répondre
à cette question, nous devons d'abord tenir compte des caractéristiques
temporelles d'une présentation multimédia. Dans le chapitre
précédent, nous avons montré que de légères
fluctuations sur l'instant de début des éléments et
sur leur durée (domaine de validité) sont tolérées.
Par exemple, la présentation d'un élément audio une
milli seconde plus tard ou plus tôt que sa date prévue n'affecte
en rien la qualité de la présentation. Ceci signifie qu'il
n'y a pas de différence perceptible si on spécifie entre
deux instants e1 et e2 la relation e1 < e2
ou e1 <= e2. De façon similaire la relation =/=
se démarque de la relation ? sur un seul instant du temps. Les quatre
relations d'instants : { <, =, >, ? } sont donc les seules qui sont
utiles pour la spécification de scénarios multimédia
[WAH 94][MIN
96].
[Table des matières]
3.2.2 Relations à base d'intervalles
Dans les relations à base d'intervalles (algèbre d'intervalles
notée IA : Interval Algebra), les relations possibles entre
deux éléments multimédia se réduisent à
toutes les combinaisons de positionnement possibles de deux intervalles
sur une droite orientée. Le modèle le plus général,
proposé par J.F. Allen [ALL 83],
dresse la liste exhaustive de toutes ces relations. La liste des combinaisons
possibles entre éléments multimédia comporte 13 relations
consistant en 7 relations de base (cf. Fig 3 ) et
de leurs relations inverses, l'égalité étant elle-même
son inverse. Ces treize relations se répartissent en deux classes,
celle des relations de séquentialité et celle des relations
introduisant le parallélisme de présentation. Dans l'avant-dernière
colonne du tableau, nous présentons la traduction de chaque relation
sous la forme d'une suite de relations à base d'instants. Les variables
x et y représentent des intervalles et les notations x-
et x+ correspondent respectivement aux instants de début
et de fin de l'intervalle x.
| Relation |
Symbole |
Inverse |
Relation à base d'instants équivalente au symbole |
Classe |
| x before y |
b |
bi |
x- < x+ < y- < y+ |
Seq |
| x meets y |
m |
mi |
x- < x+ = y- < y+ |
Seq |
| x overlaps y |
o |
oi |
x- < y-< x+ < y+ |
Par |
| y finishes x |
f |
fi |
x- < y-< x+ = y+ |
Par |
| y during x |
d |
di |
x- < y- < y+< x+ |
Par |
| x starts y |
s |
si |
x- = y-< x+ < y+ |
Par |
| x equals y |
e |
ei |
x- = y- < x+ = y+ |
Par |
Fig 3. Les relations à base d'intervalles
De façon analogue aux relations à base d'instants, il
existe 213 = 8192 relations composées. Par exemple, si
l'auteur d'un scénario veut décrire que deux intervalles
A et B sont disposés séquentiellement dans le temps, la relation
qui les lie correspond à la forme disjonctive suivante : A {b, bi,
m, mi } B. Cette relation consiste simplement à éliminer
les relations de classe parallèle.
Afin de mesurer l'apport de l'algèbre d'intervalles au multimédia,
nous commençons d'abord par la comparer avec l'algèbre d'instants.
Le tableau de la Fig 3 indique que chaque relation
primitive à base d'intervalles est équivalente à plusieurs
relations d'instants. Il est alors légitime de se demander s'il
en est de même pour les relations composées ou disjonctives
à base d'intervalles. Auquel cas, ces deux représentations
seraient équivalentes [VAN 90].
Le tableau de la figure Fig 4 donne un résumé
du nombre de relations disjonctives de IA qui peuvent être générées
à partir d'un sous-ensemble des relations composées de PA.
| Relations à base d'instants de PA |
Nombre de disjonctions de IA pouvant être générées |
| <, =, > |
13 |
| <, =, >, ? |
29 |
| <=, <, =, >, >=, ? |
82 |
| <=, <, =, >, >=, ?, =/= |
187 |
Fig 4. Relations disjonctives de IA engendrées par les relations
de PA
La dernière ligne montre que seules 187 relations sont exprimables
à partir des relations à base d'instants : c'est l'algèbre
d'intervalles restreinte qu'on notera RIA (Restricted Interval Algebra).
Ce fait témoigne de la plus grande richesse des relations de IA
par rapport à celle de PA. Sur les 8192-187 = 8004 relations non
exprimables moyennant PA, il existe plusieurs relations qui peuvent être
utiles dans un scénario multimédia. En particulier, la relation
A {b, bi, m, mi} B qui dénote l'exclusion mutuelle entre deux intervalles.
Cette relation peut être utilisée pour traduire l'impossibilité
de présenter A et B en même temps. Par exemple, si ces derniers
nécessitent la même ressource matérielle (carte de
décompression, haut-parleur, etc.).
Notons que les relations d'instants jugées utiles pour le multimédia
dans PA engendrent uniquement 29 relations d'IA (deuxième ligne
du tableau Fig 4 ). Plusieurs auteurs [MIN
96][WAH 94][SEN
96] les retiennent d'ailleurs comme une référence pour
mesurer l'expressivité d'un langage de synchronisation temporelle
multimédianote4.
[Table des matières]
3.2.3 Choix entre algèbres d'intervalles et d'instants
Dans le cadre des systèmes d'édition de documents multimédia,
plusieurs arguments plaident en faveur d'une spécification des documents
multimédia à base d'intervalles :
-
Les opérations d'édition de documents portent sur les éléments
de base ou composés dont la projection dans le temps correspond
à des intervalles.
-
La description du scénario est syntaxiquement plus compacte.
-
Elle répond mieux au critère d'encapsulation et de modularité
puisqu'il est possible d'une part de délimiter et de regrouper des
portions d'un scénario sous forme d'un seul intervalle fictif (sous-scène),
et d'autre part d'isoler les éléments et les relations qu'il
contient afin de le relier aux autres portions du scénario.
En revanche, la représentation à base d'instants fournit
un très bon support d'exécution pour la présentation.
En effet, on peut considérer que l'état du système
de présentation ne change pas de façon continue dans le temps
mais évolue lors de l'apparition d'événements discrets
(on parle de Système Dynamique à Événements
Discrets (SDED) [SEN 96]). Dans ce cas,
la représentation d'un scénario à base d'instants
permet de manipuler une structure interne de type graphe, qui peut être
exploitée comme une description des tâches à ordonnancer
lors de la présentation.
[Table des matières]
3.3 Expression des relations et langage temporel multimédia
Après avoir présenté et analysé la nature des
relations temporelles, nous nous proposons dans cette section d'étudier
la capacité des deux langages temporels à modéliser
un scénario multimédia. Cela revient à poser la question
: est-ce que la sémantique attachée à ces relations
est suffisante pour traduire tous les schémas de synchronisation
multimédia ?
Afin de répondre à cette question, il est nécessaire
d'analyser les différents besoins qui apparaissent lorsqu'on cherche
à spécifier un scénario multimédia. Notre analyse
nous a conduit à séparer trois types de besoins :
-
Exprimer des informations qualitatives : L'auteur doit pouvoir positionner
les éléments dans le temps en se basant uniquement sur des
informations de placement relatif, sans contraintes numériques,
par exemple x avant y.
-
Exprimer des informations quantitatives : Il doit pouvoir aussi
manipuler des informations numériques, par exemple x avant y de
3 secondes.
-
Exprimer des informations causales.
En ce qui concerne les informations causales, il est nécessaire
dans certains cas de pouvoir exprimer des scénarios dans lesquels
l'occurrence d'un instant de fin d'un élément provoque l'arrêt
d'un autre, même si ce dernier n'a pas restitué tout son contenu
à l'utilisateur. Pour le cas d'une représentation à
base d'intervalles, nous avons identifié trois relations pertinentes
de ce type :
-
La relation Parmin(A, B) dans laquelle les deux éléments
démarrent en même temps et le premier des deux éléments
qui se termine provoque la terminaison de la construction.
-
La relation Parmax(A, B) dans laquelle les deux éléments
démarrent en même temps et le dernier des deux éléments
qui se termine provoque la terminaison de la construction.
-
La relation Parmaster(Am, B) dans laquelle les deux éléments
démarrent en même temps et c'est la terminaison de l'élément
désigné par l'auteur (dans ce cas c'est Am) qui
provoque la terminaison de la construction.
À titre d'exemple, dans un scénario composé d'une
séquence vidéo et d'une séquence musicale, si l'auteur
souhaite que ces deux éléments se terminent en même
temps même s'ils ont des durées différentes, il lui
suffit d'introduire la relation Parmin(audio, vidéo). Cette relation
ne peut être exprimée ni par l'algèbre d'instants,
ni par l'algèbre d'intervalles. Si ces algèbres permettent
de construire des scénarios non interactifs, les relations causales
permettent d'intégrer une certaine forme d'interactivité.
Par exemple, si l'auteur souhaite décrire un scénario où
l'activation d'un bouton permet l'interruption d'une vidéo, il lui
suffit d'introduire la relation suivante : Parmaster(Boutonm,
vidéo).
[Table des matières]
4 Analyse et synthèse de scénarios temporels
Les problèmes liés à la représentation et à
la composition d'éléments multimédia ressemblent,
sur beaucoup d'aspects, à des problèmes rencontrés
dans d'autres domaines de l'informatique. Parmi ces domaines, les plus
proches du multimédia et plus particulièrement de l'édition
de documents, concernent la représentation et la gestion des connaissances
temporelles [MEI 92], l'ordonnancement
de tâches [MAC 85] et la planification
[VID 95b]. Parmi ces travaux, l'algèbre
d'intervalles d'Allen [ALL 83] et l'algèbre
d'instants proposée par Kautz [KAU
91] ont beaucoup marqué la recherche en multimédia, en
particulier en ce qui concerne l'expression des relations temporelles,
comme nous l'avons présenté dans la section 3.2.
En revanche, les travaux portant sur la synthèse et l'analyse des
scénarios temporels, qui sont au coeur du processus d'édition,
restent de nos jours encore très peu abordés. Pourtant beaucoup
de travaux, dont ceux d'Allen [ALL 91]
et Kautz [KAU 91], ont largement étudié
ces deux aspects dans le cadre des systèmes temporels à base
de contraintes. Dans la suite de ce chapitre, nous montrons qu'ils constituent
un cadre pertinent pour aborder l'édition de documents multimédia.
Dans cette section, nous étudions les fondements théoriques
des modèles temporels basés sur les contraintes. Cette étude,
qui constitue l'originalité de notre démarche, place le problème
de l'édition multimédia comme un cas particulier appartenant
à une classe de problèmes plus généraux appelés
CSP (Constraint Satisfaction Problem).
[Table des matières]
4.1 Introduction aux CSP
Dans le domaine des CSP, la notion de contrainte désigne
un énoncé déclaratif exprimant une mise en relation
entre les données d'un problème. Une contrainte constitue
donc un élément de représentation de la connaissance
relative à un problème. Un système de gestion de contraintes
est l'outil qui permet d'une part d'exprimer dans un formalisme déclaratif
les contraintes qui décrivent un problème, et qui fournit
d'autre part des algorithmes d'analyse et de synthèse capables de
déterminer sa cohérence et de le résoudre s'il admet
une solution. L'approche fondée sur les contraintes allie donc expression
du problème (aspect langage) et techniques algorithmiques de résolution
(gestion des contraintes). Justement, ces deux éléments correspondent
parfaitement aux besoins d'édition que nous visons.
Un CSP est défini par la donnée d'un ensemble de
variables, chacune associée à un domaine de valeurs, et par
la donnée d'un ensemble de contraintes liant ces variables. Une
contrainte est généralement décrite par l'ensemble
de combinaisons de valeurs qui la satisfont. Une solution d'un CSP
est une instantiation de ces variables qui satisfait simultanément
toutes les contraintes d'un problème. Nous nous intéressons
par la suite uniquement aux CSP binaires, c'est-à-dire ne manipulant
que des contraintes entre deux variables.
Formellement, un problème de satisfaction de contraintes
binaires P = (X, D, C, R) est défini par :
-
un ensemble de variables X = {X1 , ..., Xn}
;
-
un ensemble de domaines D = {D1, ..., Dn}
où Di est le domaine de la variable Xi ;
-
un ensemble de contraintes C = {Ci,j, / 1 <=
i, j <=n } ;
-
un ensemble de relations R = {Ri,j / 1 <= i,
j <= n} ; Ri,j est l'ensemble des combinaisons de valeurs
qui satisfont la contrainte Ci,j.
Une solution sigma d'un tel CSP est définie par : sigma =
{x1 in D1, ...,xn in Dn} /
forall Ci,j in C, (xi, xj) in Ri,j
Un CSP est cohérent si et seulement si il existe au moins
une solution qui le satisfait.
On peut associer à tout CSP binaire un réseau où
les sommets sont les variables et les arcs représentent les contraintes
étiquetés par les domaines des variables. On qualifie de
minimal un tel réseau lorsque les domaines des variables
sont restreints aux seules valeurs appartenant à au moins une solution.
Dans le domaine du multimédia, les mérites que nous attribuons
à une approche fondée sur les contraintes peuvent être
résumés ainsi :
-
Elle permet une description formelle de la synchronisation temporelle
des documents multimédia.
-
Elle permet une expression déclarative de la synchronisation
temporelle. Ce type d'expression rend possible la construction de langages
de synchronisation plus faciles à utiliser que les langages impératifs
comme les scripts.
-
Elle permet à l'auteur d'un document de se focaliser sur l'édition
d'un document (la formulation de ce qu'il veut obtenir) sans se préoccuper
de la façon dont il va l'obtenir (la résolution ou le formatage).
Dans cette section, nous établissons le lien qui existe entre le
problème de synchronisation d'un document multimédia et les
systèmes de contraintes CSP. Nous commençons d'abord
par un rappel des principales définitions relatives à la
théorie des CSP. Ces définitions nous seront utiles
lorsque nous aborderons les techniques de vérification de la cohérence
d'un scénario et de recherche de solutions qui sont présentées
dans les sections 4.3 et 4.4.
[Table des matières]
4.2 TCSP : les CSP temporels
La synchronisation temporelle multimédia peut être abordée
dans le cadre d'une classe particulière des CSP désignée
par TCSP (Temporal Constraints Satisfaction Problem). Dans
cette classe, les variables modélisent des instants ou des intervalles
temporels de durée, et les relations leurs placements relatifs à
travers le temps. Il existe deux grandes familles de techniques permettant
de gérer les contraintes temporelles :
-
La gestion d'un scénario à partir de relations qualitatives
ou symboliques (TCSP symboliques).
-
La gestion d'un scénario à partir de relations quantitatives
ou numériques (TCSP numériques).
En réalité, ces deux types de représentation sont
nécessaires dans les systèmes multimédia, car dans
un processus d'édition, l'auteur peut vouloir exprimer des relations
de synchronisation sous forme symbolique, mais leurs conséquences
dans le scénario peuvent se traduire sous forme de contraintes numériques.
Ces mêmes contraintes peuvent à leur tour limiter les relations
symboliques que l'auteur peut vouloir ajouter. Ceci explique la difficulté
du problème de synchronisation des documents multimédia qui
combine ces deux types de représentation.
[Table des matières]
4.3 Gestion symbolique des relations temporelles
La gestion symbolique des contraintes temporelles, introduit par Allen,
s'appuie sur l'organisation des relations sous forme d'un graphe temporel.
Les sommets sont des symboles qui représentent des intervalles,
et les arcs sont des relations temporelles disjonctives d'IA (voir section
3.2.2).
La gestion symbolique des relations (analyse et synthèse) consiste
à appliquer un mécanisme qui s'apparente à une activité
de déduction. Ces déductions aboutissent au retrait de certaines
disjonctions des relations du graphe, ce qui revient à les préciser.
C'est cette caractéristique qui nous fait donner le nom de symbolique
à ce type de système, par opposition aux systèmes
numériques dont la gestion porte sur des contraintes numériques
(domaines de validité des intervalles).
Pour les deux types de relations à base d'instants où
d'intervalles, nous nous intéressons aux deux aspects suivants :
-
Les aspects liés à la puissance expressive des relations
symboliques.
-
Les aspects liés à la gestion des contraintes temporelles
symboliques, en particulier le problème de cohérence
d'une spécification et de recherche d'une solution.
Nous allons d'abord présenter ces deux types de langage permettant
l'expression des contraintes temporelles. En particulier, nous décrivons
les mécanismes de composition qui leur sont associés ainsi
que les avantages ou les inconvénients de gérer un document
multimédia en adoptant l'une ou l'autre des deux méthodes.
[Table des matières]
4.3.1 Loi de composition temporelle
Dans les deux algèbres d'instants et d'intervalles, chaque relation
de 2B (l'ensemble des relations composées) est
inversible et son inverse est une relation de 2B ; par
exemple, x before y est l'inverse de y before x dans l'algèbre
d'intervalles. Pour chaque relation x R y de l'ensemble 2B
entre deux éléments temporels x et y, on définit la
relation inverse notée y R-1 x.
Pour permettre de combiner des connaissances temporelles exprimées
par de telles relations, deux opérations sont définies sur
les éléments de l'ensemble 2B :
-
L'intersection intersect de deux éléments de l'ensemble
2B est un élément de l'ensemble 2B.
-
L'union union de deux éléments de l'ensemble 2B
est un élément de l'ensemble 2B.
-
De plus, ? est l'élément neutre de l'intersection
et l'élément absorbant de l'union.
-
bot est l'élément neutre de l'union et l'élément
absorbant de l'intersection.
On définit également une loi de composition interne @, associative,
non commutative d'élément absorbant ? Son élément
neutre est l'égalité (= dans PA et equals dans IA). Si R1
et R2 sont deux relations de 2B, nous obtenons une nouvelle
relation R3(x, z) = R1(x, y) @ R2(y, z) qui fait aussi partie de 2B.
Cette loi permet d'inférer, à partir de la relation R1(x,
y) et R2 (y, z) la relation R1 @ R2(x, z).
Les trois opérations, @, intersect et union sont deux à
deux distributives. Qu'il s'agisse d'instants ou d'intervalles { 2B,
union, @ } est une structure d'algèbre. C'est pour cette raison
qu'on parle d'algèbre d'instants ou d'algèbre
d'intervalles.
[Table des matières]
4.3.2 Composition dans l'algèbre d'instants
La loi de composition @ s'applique de la façon suivante dans PA.
Par exemple, si nous avons trois instants temporels x, y et z avec les
relations x < y et y = z, on déduit la nouvelle relation x <
z (voir le tableau de la Fig 5 ).
| @ |
< |
= |
> |
| < |
< |
< |
? |
| = |
< |
= |
> |
| > |
? |
> |
> |
Fig 5. Loi de composition de PA pour les relations primitives
En utilisant la distributivité de @, le même tableau peut
être utilisé pour les relations de 2B. Par
exemple, à partir des deux relations : x {<, =} y et y {<,
=} z, on déduit :
x [ {<, =} @ {<, =} ] z = x [ (<@<) union (<@=) union
(=@<) union (=@=) ] z
= x [ < union < union < union = ] z
= x [{<, =}] z
Ainsi, si l'auteur d'un document veut exprimer un scénario temporel
multimédia moyennant l'algèbre d'instants, il construit une
base d'instants temporels qui correspondent aux différents événements
du scénario. Ensuite, il les relie temporellement en spécifiant
des relations entre eux.
Par exemple, supposons que dans l'exemple de déduction ci-dessus,
l'événement x corresponde au début d'une vidéo,
y au début d'un élément audio et z au début
d'un élément texte. Nous avons montré à travers
l'exemple précédent qu'une application de la loi de composition
entre les relations interdit d'introduire la relation x > z, au risque
de rendre le scénario incohérent.
[Table des matières]
4.3.3 Composition avec l'algèbre d'intervalles
Pour faire de la vérification de cohérence, Allen suggère
[ALL 83] l'utilisation des lois de composition
appliquées aux intervalles afin d'exprimer un scénario temporel
et de raisonner à son propos. L'expression d'une relation de synchronisation
qui lie un élément temporel à un autre est alors simplement
traduite sous forme de relation symbolique entre les deux éléments.
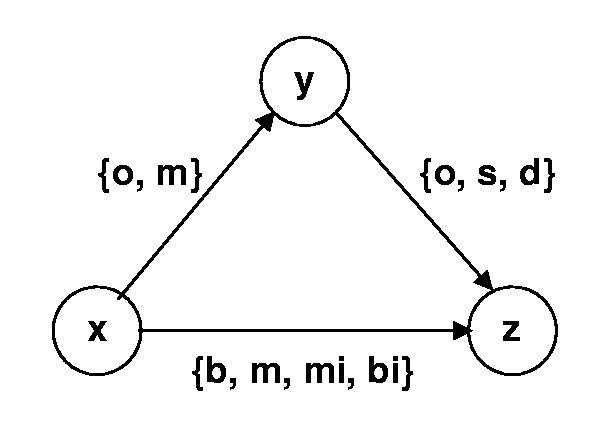Fig 6. Graphe de contraintes de l'exemple 1
Exemple 1 : Soient trois éléments multimédia
x, y et z. Supposons que l'auteur d'un scénario veut exprimer les
contraintes temporelles suivantes (voir Fig 6 ) :
-
L'élément x chevauche temporellement y ou démarre
juste avant :
x {o, m} y.
-
L'élément x ne se joue pas en même temps que l'élément
z :
x {b, m, mi, bi} z.
-
L'élément y chevauche, démarre en même temps
ou se joue pendant l'élément z :
y {o, s, d} z.
Comme pour l'algèbre de points, le pouvoir de déduction du
système d'Allen repose sur l'établissement d'une table de
transitivité 7x 7 (voir Fig 7 ) entre les relations
primitives, permettant de calculer R3 dans la formule :
x R1 y @ y R2 z Rightarrow x R3 z
En général, la relation R3 est disjonctive, car la connaissance
de R1 et de R2 ne donne pas toujours assez d'information pour que R3 soit
suffisamment précise.
Lorsque R1 et R2 sont elles-mêmes disjonctives, l'algorithme de
calcul de R3 est très simple :
-
Décomposer R1 et R2 en une disjonction de relations élémentaires.
-
Développer tous les termes en appliquant la distributivité
de intersect par rapport à union. On obtient ainsi des clauses qui
sont des paires conjonctives.
-
Calculer grâce à la table de la Fig 7
le résultat de chaque paire conjonctive.
-
Les conjonctions ayant disparu, composer les clauses disjonctives en une
seule relation composée.
|
R1 @ R2
|
b
|
m
|
s
|
f
|
d
|
o
|
e
|
|
b
|
b
|
b
|
b
|
b
|
b,m,s,d,o
|
b
|
e
|
|
m
|
b
|
b
|
m
|
b,m,s,d,o
|
s,d,o
|
b
|
b
|
|
s
|
b
|
b
|
s
|
d
|
d
|
b,m,o
|
m
|
|
f
|
b
|
m
|
d
|
f
|
d
|
s,d,o
|
s
|
|
d
|
b
|
b
|
d
|
d
|
d
|
b,m,s,d,o
|
f
|
|
o
|
b
|
b
|
o
|
s,d,o
|
s,d,o
|
b,m,o
|
d
|
|
e
|
b
|
m
|
s
|
f
|
d
|
o
|
o
|
Fig 7. Loi de composition d'IA
L'algorithme proposé par Allen permet la détection d'incohérences
temporelles. Son principe est le suivant : à partir de la table
de transitivité ci-dessus, on calcule toutes les relations induites
et on les confronte aux relations existantes, ceci permet d'obtenir des
relations déduites, plus précises. L'algorithme propage ces
relations par application d'une autre transitivité et ainsi de suite
jusqu'au repos.
Ce principe s'applique pour les deux types de relations, d'instants
ou d'intervalles. Dans les deux cas, le problème est représenté
sous forme d'un graphe (S, R) où S={Xi,...,Xj}
est l'ensemble des variables et Ri,j est l'ensemble des contraintes
entre les variables X i et Xj. L'algorithme nécessite
un graphe complet : les arcs entre variables qui ne sont liées initialement
par aucune relation sont étiquetées par la relation ?
Initialisation : Pour i, j in [1, n], i =/= j :
Q <== {i, j} Q est la pile des relations en cours de propagation
Propagation : Tant que Q =/= emptyset
1) {i, j} <== dépiler(Q) On considère un arc
2) Pour k in [1, n], k =/= i, j
- On calcule l'influence de l'arc courant sur les autres arcs
R'ik<== ( Rij @ Rjk ) intersect
Rik R'kj<== ( Rki @ Rij
) intersect Rkj
- Si R'ik ou R'kj = bot
Alors STOP nous avons détecté une incohérence
- Si la nouvelle relation diffère de l'ancienne, il faut la
propager Si R'ik =/= Rik Alors empiler
{i, k} dans Q; Rik <== R'ik Si R'kj
=/= Rkj Alors empiler {j, k} dans Q; Rkj <== R'kj
Cet algorithme permet de préciser de plus en plus le graphe en
éliminant des disjonctions. Étant donné que le nombre
de relations et la taille du graphe sont finis, et que ce graphe est borné
inférieurement par le graphe minimal, l'algorithme s'arrête
toujours : soit parce qu'il n'y a plus de relations apportant une information
nouvelle, soit parce qu'une relation composée devient vide, auquel
cas on a détecté l'incohérence du scénario.
L'application de cet algorithme à l'exemple 1 aboutit à
la suppression de trois relations incohérentes (voir les relations
barrées de la Fig 8 ). Cette méthode
d'analyse a été proposée pour les documents multimédia
par Kshirasagar [KSH 94].
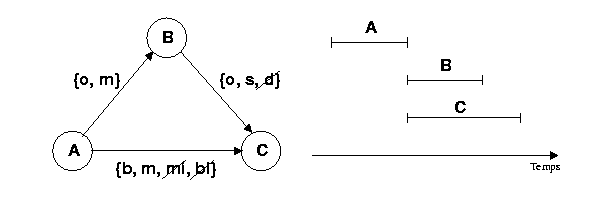Fig 8. Graphe minimal et scénario cohérent pour l'exemple
1
[Table des matières]
4.3.4 Discussion
L'approche proposée par Allen [ALL
83] constitue le principal travail accompli dans le cadre de la résolution
d'un TCSP symbolique. Cet algorithme, polynômial, n'est malheureusement
pas complet. En effet, Vilain et Kautz [VIL
86] ont montré que l'algorithme d'Allen pouvait ne pas détecter
certaines incohérences et que le problème d'existence d'une
solution dans IA est NP-complet. Ce qui signifie que, pour rechercher une
solution, il faut utiliser des méthodes de recherche exhaustives.
Ces techniques, même appliquées à des problèmes
de petite taille, restent pour le cas des systèmes multimédia
coûteuses car elles sont de complexité exponentielle.
En conclusion, si le modèle proposé par Allen permet une
représentation plus riche que la représentation à
base d'instants, c'est au prix de l'incomplétude et d'un accroissement
important de la complexité algorithmique.
[Table des matières]
4.4 Gestion numérique des relations temporelles
Contrairement à l'approche symbolique, les systèmes numériques
manipulent explicitement des nombresnote5,
ce qui leur permet de couvrir l'aspect métrique du temps. Le modèle
précédent représente et traite le temps uniquement
à travers une représentation symbolique (traitement qualitatif).
Cette représentation bien que très utile pour l'édition
ne prend pas en compte des informations numériques. En particulier,
dans la construction d'un scénario, on peut être intéressé
par les trois opérations suivantes :
-
Déterminer si un scénario est quantitativement cohérent
: étant donné les valeurs possibles des durées
des intervalles, il existe une valuation de ces durées qui satisfait
toutes les contraintes.
-
Retrouver toutes les valeurs d'un intervalle susceptibles de figurer dans
une solution : c'est la contrainte numérique minimale. Cette donnée
permet d'indiquer à l'auteur, compte tenu des contraintes déjà
introduites, dans quelle mesure il peut modifier la durée d'un intervalle
tout en préservant la cohérence du scénario.
-
Effectuer le formatage temporel, ce qui revient à trouver une solution
spécifique pour un scénario cohérent donné.
[Table des matières]
4.4.1 Réseaux de contraintes numériques TCSP et STP
Les contraintes temporelles liées aux domaines de validité
et aux relations temporelles symboliques peuvent s'exprimer sous forme
de différences bornées entre dates d'instants. En partant
de cette constatation, Dechter et Meiri [DEC
91] proposent de représenter les problèmes temporels
sous forme de TCSP numériques.
Un TCSP numérique est défini par un ensemble de
variables X1, .., Xn représentant des instants
ayant des valeurs de dates dans aleph, et un ensemble de contraintes binaires.
Une contrainte Ci,j entre les variables Xi et Xj,
est une disjonction de différences bornées du type :
a1i,j <= Xi -Xj <=
b1i,j wedge ... wedge ani,j
<= Xi -Xj <= bni,j
Par conséquent, une contrainte Ci,j définit
un ensemble d'intervalles de validité {I1i,j,
..., In i,j} où Ik i,j
= [aki,j, bki,j ]. Un élément
multimédia peut donc être modélisé dans ce formalisme
par une union de domaines de validité. En fait, le seul cas de TCSP
qui peut être résolu en temps polynômial est celui d'un
TCSP ne comportant qu'un intervalle par arc (le problème
STP : Simple Temporal Problem). Cela correspond à
la modélisation de chaque élément multimédia
par un seul domaine de validité. Pour cette raison, nous allons
nous restreindre dans la suite de cette étude aux cas des STP.
Le problème de satisfaction de contraintes se présente
dans les STP par un graphe conjonctif de différences bornées.
Dans ce type de graphe, chaque arc reliant deux instants temporels i et
j est étiqueté par des bornes [aij , bij]
et indique la présence d'une contrainte de distance entre i et j
:
aij <= Xi -Xj <= bij
Cette contrainte peut aussi être décrite par une paire
d'inégalités :
Xi -Xj <= bij
et Xi -Xj <= -aij
Chaque contrainte Cj, i d'un sommet j à un sommet
i peut être retrouvée à partir de Ci, j
: Cj, i = [-bij , -aij], en général
une seule de ces contraintes est représentée dans le graphe.
De plus, un instant particulier, défini par le sommet 0 et la variable
X0 est ajouté au graphe pour représenter le début
du scénario. Toutes les valeurs Xi sont définies
par rapport à X0 et chaque contrainte C0, i
représente la contrainte de distance par rapport au début
du scénario, on notera cette contrainte Ci et on considère
pour des raison de simplicité que X0 = 0.
En conséquence, la résolution d'un problème STP
revient à la résolution d'un problème décrit
par ensemble d'inéquations linéaires sur les variables X0,
..., Xn.
[Table des matières]
4.4.2 Systèmes utilisant la programmation linéaire
Le problème de résolution d'un système linéaire
d'inégalités est bien connu dans le domaine de la recherche
opérationnelle. Il peut en effet être résolu en temps
exponentiel moyennant l'algorithme du simplex [DAN
62] ou par l'algorithme de Khachiyan [KHA
79]. L'algorithme du simplex optimise n'importe quelle fonction linéaire
sur un domaine exprimé au moyen de contraintes linéaires.
Dans le problème d'analyse d'un scénario, il n'y a a priori
pas de fonction à optimiser. On cherche seulement à définir
les domaines de validité des éléments multimédia
pour le scénario en construction. Par contre, pour le formatage
on peut toujours considérer qu'une solution qui s'écarte
le moins possible des valeurs optimales des éléments est
celle qu'il faut rechercher en priorité. Dans ce cas, il est possible
de définir une fonction coût, à minimiser, qui permet
de guider le choix de la solution. S'il n'existe pas de solution, l'ensemble
de contraintes est incohérent. De plus, on a toujours "sous la main"
une solution totalement explicitée, mais les domaines des variables
eux ne sont pas explicites. Par conséquent, l'auteur ne sait pas
dans quelle mesure les valeurs des variables dans la solution exhibée
sont modifiables tout en restant une solution au problème.
Ce genre de méthodes permet d'utiliser toute la puissance de
représentation de l'algèbre linéaire. Un point révélateur
est que les contraintes sont rarement présentées du point
de vue d'un graphe temporel. De plus, on ne peut pas vraiment considérer
le simplex comme une méthode d'analyse de scénarios, dans
la mesure où l'algorithme ne fait qu'exhiber une solution. Dans
le cas d'incohérence, l'algorithme rejette en bloc l'ensemble des
contraintes, ce qui empêche l'auteur de localiser avec précision
la source de l'incohérence.
Quant à la complexité de cette méthode, elle est
fortement alourdie par le coût théoriquement exponentiel de
l'algorithme du simplex, qu'il faut faire fonctionner chaque fois que l'on
ajoute une contrainte (il n'est pas incrémental). C'est cette solution
qui a été adoptée dans les deux seuls systèmes
multimédia ayant implanté un module de recherche automatique
de solution ou formateur temporel multimédia : Firefly [BUC
93] et plus récemment Isis [KIM
95].
[Table des matières]
4.4.3 Systèmes basés sur les réseaux de contraintes
Nous avons vu que non seulement les relations temporelles s'expriment de
façon linéaire, mais aussi que les intervalles de validité
peuvent être représentés de la même façon
(inégalités sur la distance entre instants de début
et fin). Les approches reposant sur les réseaux de contraintes partent
du constat que les STP admettent des solutions plus efficaces que
celles présentées dans la section précédente
: les inéquations représentant les contraintes temporelles
sont structurées sous forme d'un graphe auquel une algorithmique
de graphe peut être appliquée.
Formellement, à chaque problème STP est associé
un graphe étiqueté orienté appelé graphe de
distance :
Définition 1 : Un graphe de distance temporelle Gd
= (V, Ed) est défini par un ensemble de sommets 0, ..,
n représentant des variables V = {X0, ..., Xn}
et un ensemble d'arcs Ed, où chaque arc Xi
==> Xj relie deux sommets distincts Xi et Xj
du graphe. Chaque arc est étiqueté par une valeur entière.
Si [ai,j,bi,j] est l'intervalle de validité
associé à la distance entre Xi et Xj,
alors l'arc Xi ==> Xj est étiqueté
par bi,j et l'arc Xj ==> Xi est étiqueté
par -ai,j.
Chaque chemin d'un sommet i à un sommet j dans le graphe Gd,
i = i0, ..., ik = j, introduit la contrainte temporelle
suivante sur la distance Xj - Xi :
Xi -Xj <=Sj = 1kaij-1, ij
S'il existe plus d'un chemin de i à j, alors il est facile de
vérifier que l'intersection de toutes les contraintes de chemins
donne :
Xj - Xi <= dij
Où dij représente la durée du plus court
chemin entre i et j. En se basant sur cette observation, la condition fondamentale
suivante pour la cohérence d'un problème STP peut
être établie :
Théorème : (Shostak [SHO
81], Liao et Wong [LIA 93], Leiserson
et Saxe [LEI 93]) Un STP est
cohérent si et seulement si son graphe de distance Gd
ne contient pas de cycle négatifs.
Preuve : Supposons qu'il existe un chemin négatif C formé
des sommets i1, i2, ..., ik=i1.
La somme des inégalités le long du chemin C donne :
Xi1 - Xi1 < 0, qui ne peut évidemment
pas être satisfaite.
Dans l'autre sens de l'équivalence, s'il n'existe aucun cycle
négatif dans Gd, alors le plus court chemin entre chaque
paire de sommets est bien défini. Pour chaque paire de sommets i
et j, le plus court chemins satisfait d0j <= aij
+ d0i ; d'où,
d0j - d0i <= aij
Donc le tuple (d01 , ... , d0n) est une solution
du STP.
Corrolaire : Soit Gd le graphe de distance d'un STP
cohérent. Il existe aux moins deux scénarios cohérents
qui sont :
S1 = (d01 , ... , d0n) et S2
= (-d10 , ... , -dn0)
Ces deux scénarios représentent une instantiation des
variables à leur date d'occurrence au plus tôt et au plus
tard respectivement.
Deux problèmes STP sont dits équivalents s'ils
représentant le même ensemble de solutions, et un STP
est dit minimal s'il n'existe aucun STP équivalent dont les
contraintes soient plus restrictives.
Algorithmes utilisant les graphes
Le graphe de distance d'un STP peut être construit en appliquant
l'algorithme du plus court chemin (all pairs shortest paths) de
Floyd-Warshal [PAP 82]. Cet algorithme
peut être considéré comme un algorithme de relaxation
: à chaque pas la valeur d'un arc est mise à jour d'un montant
qui dépend uniquement de celles des arcs adjacents.
Algorithme du plus court chemin
1. Pour i := 1 à n faire dii <== 0
2. Pour i, j := 1 à n faire dij <== aij
3. Pour k := 1 à n faire
4. Pour i, j := 1 à n faire
5. dij <== min {dij, dik + dkj
}
Fig 9. Algorithme all pairs shortest paths
L'algorithme s'exécute en O(n3) et détecte
les cycles négatifs simplement en examinant le signe des éléments
diagonaux dii.
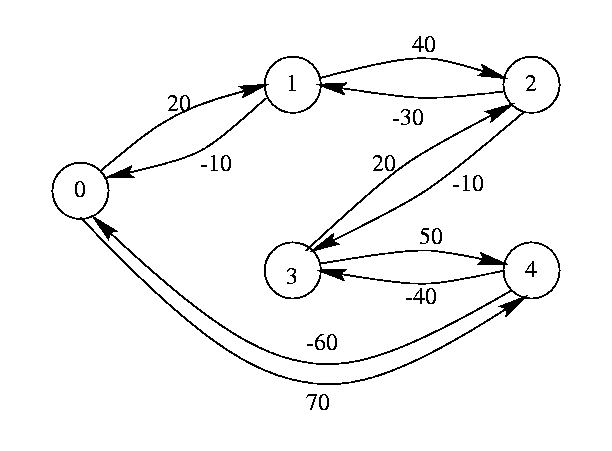
Considérons l'exemple de la Fig 10 , puisqu'il
n'y a pas de cycle négatif, le STP correspondant est cohérent.
Les plus courts chemins dij sont présentés dans
le tableau suivant :
 |
|
0 |
1 |
2 |
3 |
4 |
| 0 |
0 |
20 |
50 |
30 |
70 |
| 1 |
-10 |
0 |
40 |
20 |
60 |
| 2 |
-40 |
-30 |
0 |
-10 |
30 |
| 3 |
-20 |
-10 |
20 |
0 |
50 |
| 4 |
-60 |
-50 |
-20 |
-40 |
0 |
|
Fig 10. Longueur des chemins les plus courts de l'exemple
L'algorithme de Floyd-Warshal constitue ainsi un algorithme polynômial
pour déterminer la cohérence du STP et le calcul des
domaines de validité minimaux et donc le graphe minimal. Une fois
que ce graphe est disponible, l'instantiation d'une solution ou le formatage
temporel peut prendre O(n2), car chaque instantiation d'une
valeur doit être conforme aux instantiations précédentes
et ne sera plus modifiée ultérieurement (cf. section 4.4.4).
Algorithmes manipulant explicitement les domaines de validité
Cette classe d'algorithmes est très proche d'une formalisation
du type étiquetage cohérent du graphe introduit par Allen
(sans que leurs concepteurs n'en fassent mention toutefois). Les variables
sont les arcs du graphe qui représentent les domaines de validité
des intervalles contrairement au cas d'Allen où elles représentaient
des relations et à l'algorithme de Floyd-Warshal où les étiquettes
représentaient des entiers relatifs. En réalité, il
existe toute une famille d'algorithmes de ce type développés
dans le cadre des systèmes à base de contraintes [MEI
92] [VID 95b]. Dans cette étude,
nous allons seulement en présenter un, appelé PC-2 [MAC
85], qui est représentatif de cette classe d'algorithmes et
qui permet d'illustrer leur principe de fonctionnement.
Algorithme PC-2 ( Macworth [MAC
85])
1. Initialisation
2. Q <== Graphe initial
3. Propagation
4. Tant que Q =/= emptyset Faire
5. 1) extraire un élément de {i, j} <== Q
6. 2) Pour k = 1 à n, k =/= i, j Faire
7. D'ik <== Dij @ Djk
+ Dik
8. D'kj <== Dki @ Dij
+ Dkj
9. - Si D'ik ou D'kj = bot
Alors Stop : une incohérence a été détectée
10. - Si D'ik =/= Dik Alors empiler
{i, k} dans Q ; Dik <== D'ik
11. - Si D'kj =/= Dkj Alors empiler
{j, k} dans Q ; Dkj <== D'kj
Fig 11. L'algorithme PC-2
Dans PC-2, la vérification de la cohérence du graphe se
fait en même temps que le calcul du graphe minimal. Le graphe minimal
est obtenu en appliquant des opérations algébriques sur les
domaines de validité. Ces opérations permettent à
chaque étape d'éliminer les valeurs impossibles d'un domaine
de validité. Soient deux domaines de validité : D1 = [d1min,
d1max] et D2 = [d2min, d2max]. On définit
les deux opérations suivantes :
À l'échelle du graphe tout entier, une modification d'un
domaine de validité peut donc en entraîner une autre. On propage
donc ces modifications jusqu'à ce que le réseau soit au repos,
ou que l'on détecte une incohérence.
La complexité de l'algorithme PC-2 est cubique O(n3).
PC-2 possède une propriété intéressante qui
consiste à réexaminer le graphe localement d'abord. En effet,
il arrive souvent que l'insertion d'un élément ou d'une relation
n'affecte qu'une portion limitée du graphe, auquel cas, il n'est
pas utile de le remettre en cause dans sa totalité (voir les lignes
10-11 de l'algorithme qui permettent d'anticiper dans ces cas l'arrêt
de l'algorithme), contrairement à l'algorithme de Floyd-Warshal
où chaque modification nécessite de reconsidérer tout
le graphe.
[Table des matières]
4.4.4 Décomposabilité d'un STP
A partir de la discussion précédente, nous avons établi
que la spécification d'un scénario peut se ramener au maintien
de la structure d'un graphe. Ce graphe est une représentation plus
explicite, puisqu'il ne retient que les domaines de validité susceptibles
de figurer dans une solution.
Étant donné un graphe cohérent, la présentation
du scénario correspondant nécessite le choix d'une solution
spécifique parmi celles qui sont possibles : c'est l'opération
de synthèse ou formatage. Les problèmes STP possèdent
une propriété importante permettant la recherche efficace
d'une solution : la décomposabilité. Un réseau
de contraintes STP est dit décomposable si chaque instantiation
d'une valeur de durée pour un élément n'est jamais
remise en cause lors du choix des valeurs des durées des autres
éléments du scénario.
Le théorème proposé par Meiri établit que
tout réseau de contraintes STP est décomposable. C'est
un résultat fondamental sur lequel repose notre mise en oeuvre.
Théorème de décomposabilitié (Meiri
[MEI 92]) : Tout problème STP
est décomposable par rapport aux contraintes décrites par
son graphe minimal de distance.
Preuve : Il suffit de montrer qu'une instantiation quelconque
d'un sous-ensemble S de k variables qui représentent des dates d'instants
(1 <= k < n) et qui satisfait tous les plus courts chemins appliqués
à S est extensible à n'importe quelle autre variable. On
procède par induction sur midSmid= k.
Pour midSmid=1, S consiste à instancier une variable unique Xi
= xi. Pour n'importe quelle variable Xj, nous devons
montrer qu'il est possible de trouver une valeur Xj = v qui
satisfait les contraintes du plus court chemin entre ces deux variables.
La valeur v doit satisfaire :
-dji <= v - xi <= dij (1)
Puisque tous les cycles du graphe de distance sont non-négatifs,
nous avons :
dji + dij >= 0
Donc, il existe au moins une valeur v qui satisfait (1)
Pour midSmid = k, supposons que le théorème est vrai pour
midSmid= k-1, et montrons qu'il reste vrai pour midSmid= k : soit S = {X1,
..., Xk} et soit {Xi = xi | 1 <= i
<= k } des instantiations qui satisfont les contraintes des plus courts
chemins entre les variables de S. Soit Xk+1not in S. Nous devons
trouver une valeur Xk+1= v qui satisfait les contraintes des
plus courts chemins entre Xk+1 et toutes les variables de S.
La valeur v doit donc satisfaire :
v - xi <= di, k+1
xi - v <= d k+1, i
Pour =1, ..., k ou encore
v <= min{ xi+ di, k+1 | 1 <= i <= k },
v >= max{ xi+ dk+1, i | 1 <= i <= k },
Supposons que le minimum est atteint à i0 et le maximum
à j0. En conséquence, v doit satisfaire :
xj0 - d k+1, j0 <= v <= xi0 +
d i0, k+1 (2)
Puisque xi0 et xj0 satisfont les contraintes du
plus court chemin, nous avons :
xj0 - xi0 <= d i0, j0
xj0 - d k+1, j0 <= v <= xi0 +
d i0, k+1
Ceci ,avec di0, j0 <= d i0, k+1 + d k+1,
j0 donne :
xj0 - d k+1, j0 <= xi0 + d i0,
k+1
Donc, il existe bien une valeur v qui satisfait les conditions de (2)
L'importance de la propriété de décomposabilité
pour le multimédia est double :
-
Le formatage pour la présentation peut être facilité,
puisque la construction de la solution peut être effectuée
sans retour arrière (sans remise en question des instantiations
précédentes).
-
L'ordre d'instantiation des variables n'étant pas important, on
peut définir plusieurs politiques de priorités lors du choix
d'une solution. On peut, par exemple, commencer par les variables qui représentent
des éléments multimédia ayant un réel contenu
(audio, vidéo, etc.) en respectant le plus possible leurs valeurs
optimales, les variables qui correspondent à de simples délais
étant choisies en seconde priorité.
Ce résultat peut avoir des implications importantes sur l'organisation
d'une application de présentation multimédia. En effet, un
STP étant décomposable, l'opération de formatage (en
particulier la politique adoptée pour réaliser le formatage)
peut être effectuée aussi bien à l'édition que
pendant l'exécution de la présentation (formatage dynamique).
Cette possibilité est particulièrement intéressante
pour des systèmes qui permettent de produire dynamiquement des parties
de scénarios [DAL 96].
[Table des matières]
4.5 Synthèse des techniques multimédia existantes
À la différence des systèmes présentés
dans le chapitre précédent où il s'agissait de décrire
les caractéristiques fonctionnelles des outils d'édition,
nous évaluons dans cette section les modèles temporels qui
sont proposés pour les documents multimédia. Cette évaluation
est basée sur un ensemble de critères introduits dans les
sections précédentes comme la représentation de l'unité
temporelle de base, le type de relations temporelles utilisées,
leur sémantique (qualitative, quantitative, causale) et la structure
des scénario considérés. À ces critères,
nous ajoutons les suivants, qui sont à prendre en compte aussi bien
dans la phase d'édition que dans la phase de présentation
:
-
L'existence de mécanismes d'analyse pour déterminer d'une
part la cohérence d'un scénario et d'autre part les domaines
de validité (valeurs pour lesquelles on peut effectivement trouver
un scénario cohérent).
-
L'existence de mécanismes de synthèse pour trouver une solution
particulière (c'est l'opération de formatage temporel).
-
Les performances, c'est-à-dire le temps de mise à jour d'un
scénario et éventuellement de la vérification de sa
cohérence et du formatage qui sont induits.
-
L'incrémentalité des opérations de mise à jour,
ce qui consiste à fournir des mécanismes d'analyse et de
synthèse applicables à chaque opération d'édition
sans remettre en cause la totalité du scénario.
-
La distinction dans le modèle entre les intervalles déterministes
et les intervalles indéterministes (indéterminisme vs. flexibilité).
| Modèle temporel |
Timeline |
Höpner & AHM |
OCPN |
Firefly & Isis |
| Technique de représentation |
Axe de temps absolu |
Expressions de parcours |
Réseau de Pétri |
Réseau de points |
| Représentation de l'unité temporelle de base |
instant |
intervalle |
intervalle |
instant |
| Expression des relations |
Implicite (datation) |
Séquence & Parmin & Parmax |
13 IA |
3 PA |
| Sémantique des relations |
quantitative |
causale |
qualitative |
qualitative quantitative |
| Structure du scénario |
Non |
Arbre |
Arbre |
Graphe |
| Analyse : Cohérence Domaines valides |
-note6 - |
Non - |
Non Oui |
Oui Non |
| Synthèse (formatage) |
- |
- |
Non |
Simplex |
| Performances |
- |
- |
- |
Très faibles |
| Incrémentalité |
Oui |
Oui |
Non |
Non |
| Indéterminisme vs Flexibilité |
Non |
Non |
Non |
Non |
Fig 12. Évaluation des principaux modèles de synchronisation
multimédia
Les modèles proposés n'abordent, comme le montre le tableau
de la Fig 12 , qu'une partie des problèmes
posés. La complexité de conception d'un système d'édition
multimédia complet apparaît clairement dans la diversité
des aspects mis en avant. En particulier, les méthodes de construction
d'un document, de vérification de la cohérence et de formatage
temporel s'adaptent peu à un processus interactif d'édition.
[Table des matières]
5 Conclusion
Dans ce chapitre, nous avons présenté les principaux aspects
liés à la modélisation des documents multimédia.
En partant d'une modélisation des éléments par des
intervalles de validité et d'une étude des relations multimédia,
nous avons montré que le problème de spécification
d'un scénario multimédia peut se ramener à un système
de contraintes de type STP. Les STP qui reposent sur l'algèbre
d'instants ou, ce qui revient au même, sur l'algèbre d'intervalles
restreinte, semblent être le meilleur compromis entre efficacité
et pouvoir de représentation.
L'approche fondée sur les contraintes est attrayante sur plus
d'un aspect. En effet, elle apporte des techniques de vérification
de la cohérence et d'analyse d'un scénario adaptées
pour le traitement de l'aspect qualitatif et quantitatif du temps. Le formatage
(ou la recherche de solution) se trouve aussi simplifié grâce
à la propriété de décomposabilité. Il
reste cependant plusieurs questions en suspend qui ne sont pas abordées
et que nous allons tenter de compléter dans la suite. Ces questions
concernent principalement :
-
La causalité et l'indéterminisme temporel, jusque là
ignorés par les modèles existants.
-
La construction incrémentale d'un scénario temporel dans
le cadre d'un système d'édition.
Notes :
(1)
On parle aussi d'événements dans certains systèmes.
(2)
Nous reviendrons dans la section 4 sur la justification
de ce terme d'algèbre.
(3)
Cette relation traduit l'impossibilité de relier temporellement
deux instants : l'incohérence.
(4)
Nous renvoyons le lecteur à ces travaux pour une étude
plus détaillée de ces 29 relations.
(5)
Dans notre cas, on s'intéresse uniquement à des nombres
entiers
(6)
«-» désigne une information non précisée
ou non considérée dans le modèle.